Asymptotic Analysis
The method of defining the mathematical bound of its run-time performance to easily conclude the average case, best case, and the worst-case scenario of an algorithm, is called the asymptotic analysis of the algorithm, in mathematical analysis. In simple words, the asymptotic analysis of the algorithm is used to mathematically calculate the running time of any operation inside an algorithm.
Example:
If the running time of one operation is x(n), it means that the running time will increase linearly with an increase in ‘n’ for the first operation. Now, for the second operation, the running time is calculated as f(n2), i.e., the running time will increase exponentially for the second operation. And, if the value of n is significantly small, the running time of both operations will be the same.
The time required by an algorithm:
It usually comes under three types:
- Worst case: Used to specify the input for which the algorithm takes a maximum time.
- Average case: Used to take the average time for the program execution.
- Best case: Used to specify the input for which the algorithm takes the minimum time.
Asymptotic Notations:
For calculating the running time complexity of an algorithm the asymptotic notations that are commonly used are:
- Big oh Notation (Ο)
- Omega Notation (Ω)
- Theta Notation (θ)
Big oh Notation (O):
The Big Oh Notation (O) is a formal way to express the upper boundary of an algorithm running time which is used to measure the worst case of time complexity or the longest amount of time, the algorithm takes to complete its operation.
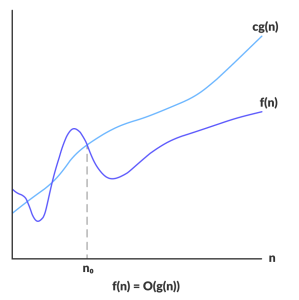
For a given function g(n), we denote 0(g(n)) with following set of functions:
O(g(n)) = { f(n): there exist positive constants c and n1
such that 0 <= f(n) <= c*g(n) for all n >= n1}
Omega Notation (Ω):
Omega Notation (Ω) is the formal way of representing the lower bound of an algorithm’s running time that is used to measure the best amount of time an algorithm can possibly take to complete or the best case time complexity.
The big- Ω notation or the Greek letter “omega” is used to bound the growth of running time for large input size and to ensure that an algorithm takes at least a certain amount of time without using an upper bound. The running time is at least k? f(n) for constant (k), for the larger value of n, if running time is Ω (f(n)).
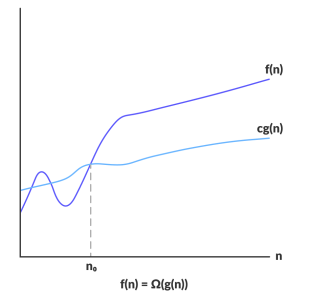
For a given function g(n), we denote Ω(g(n)) with the following set of functions:
Ω(g(n)) = {f(n): there exist positive constants c and n1
such that 0 <= c*g(n) <= f(n) for all n >= n1}
Theta Notation (θ):
Theta Notation (θ) is the formal way to express both the upper bound and lower bound of an algorithm running time. The running time is at most k2-n and at least k1 θn for some constants k1 and k2 if the running time of an algorithm is θ (n), and if at once (n) gets large enough.
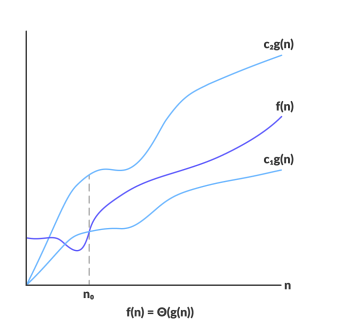
For a given function g(n), we denote θ(g(n)) with the following set of functions :
θ(g(n)) = {f(n): there exist positive constants c1, c2 and n0
such that θ <= c1*g(n) <= f(n) <= c2*g(n) for all n >= n1}
Commonly Used Asymptotic Notations:
| constant | O(1) |
| linear | O(n) |
| logarithmic | O(log n) |
| n log n | O(n log n) |
| exponential | 2Ο(n) |
| cubic | Ο(n3) |
| polynomial | nΟ(1) |
| quadratic | Ο(n2) |