[ad_1]
Copilot, Codex, and AlphaCode: How Good are Computer Programs that Program Computers Now?
Enabled by the rise of transformers in Natural Language Processing (NLP), we’ve seen a flurry of astounding deep learning models for writing code in recent years. Computer programs that can write computer programs, generally known as the program synthesis problem, have been of research interest since at least the late 1960s (pdf) and early 1970s.
In the 2010s and 2020s, program synthesis research has been re-invigorated by the success of attention-based models in other sequence domains, namely the strategy of pre-training massive attention-based neural models (transformers) with millions or billions of parameters on hundreds of gigabytes of text.
The pre-trained models show an impressive capacity for meta-learning facilitated by their attention mechanisms, and can seemingly adapt to a textual task with only a few examples included in a prompt (referred to as zero-shot to few-shot learning in the research literature).
Modern Program Synthesis With Deep NLP Models
NLP models can further be trained with specialized datasets to fine-tune performance on specific tasks, with writing code a particularly interesting use case.
GitHub Copilot, billed as “Your AI Pair Programmer,” caused no small amount of controversy when it was introduced in June 2021. In large part this was due to the use of all public GitHub code in the training dataset, including projects with copyleft licenses that may disallow the use of the code for projects like Copilot, unless Copilot itself were to be made open source, according to some interpretations.
Copilot is the result of the relationship between OpenAI and Microsoft, based on a version of GPT-3 trained on code. The version demonstrated by OpenAI and available via their API is called Codex. Formal experiments with Copex are described in Chen et al. 2021.
Not to be outdone, in early 2022 DeepMind upped the stakes with their own program synthesis deep NLP system: AlphaCode.
Here Comes a New Challenger: AlphaCode
Like Codex and Copilot before it, AlphaCode is a large NLP model designed and trained to write code. Rather than trying to build AlphaCode as a productivity tool for software engineers like Copilot, AlphaCode was developed to take on the challenge of human-level performance in competitive programming tasks.
The competitive coding challenges used to train and evaluate AlphaCode (making up the new CodeContests dataset) lie somewhere between the difficulty level of previous datasets and real-world software engineering.
For those unfamiliar with the competitive coding challenge websites, the task is somewhat like a simplified version of test-driven development. Based on a text description and several examples, the challenge is to write a program that passes a set of tests, most of which are hidden from the programmer.
Ideally, the hidden tests should be comprehensive, and passing all tests should be representative of solving the problem, but covering every edge case with unit tests is a difficult problem. An important contribution to the program synthesis field is actually the CodeContests dataset itself, as the DeepMind team made significant efforts to reduce the rate of false positives (tests pass but the problem is unsolved) and slow positives (tests pass but the solution is too slow) by generating additional tests through a process of mutation.
AlphaCode was evaluated on solving competitive coding challenges from the competition website CodeForces, and overall AlphaCode was estimated to perform in the “top 54.3
Note that the metric may be a bit misleading, as it actually equates to performance in the 45.7th percentile. While the ~45th percentile sounds decidedly less impressive, it’s incredible that the AlphaCode system was able to write any algorithms that passed every hidden test at all. But AlphaCode used a very different strategy to solving programming problems than a human would.
While a human competitor might write an algorithm that solves most of the examples and iteratively improve it until it passes all tests, incorporating insights from running early versions of their solution, AlphaCode takes a more broad-based approach by generating many samples per problem and then choosing ~10 to submit.
A big contributor to AlphaCode’s performance on the CodeContests dataset is the result of post-generative filtering and clustering: after generating some 1,000,000 candidate solutions, AlphaCode filters the candidates to remove those that don’t pass the example tests in the problem statement, eliminating around 99
The authors mentioned that around 10
The remaining candidates are then winnowed down to 10 submissions or less by clustering. In short, they trained another model to generate additional test inputs based on the problem description (but note they do not have valid outputs for these tests).
The remaining candidate solutions, which may number in the 1000s after filtering, are clustered based on their outputs on the generated test inputs. A single candidate from each cluster is selected for submission, in order from largest to smallest clusters. Clusters are sampled more than once if there are fewer than 10 clusters.
While the filtering/clustering step is unique and AlphaCode was fine-tuned on the new CodeContests dataset, it was initially trained in much the same way as Codex or Copilot. AlphaCode first underwent pre-training on a large dataset of publicly available code from GitHub (retrieved on 2021 July 14th). They trained five variants of 284 million to 41 billion parameters.
In the same spirit as the AlphaGo lineage or Starcraft II-playing AlphaStar, AlphaCode is a research project aiming to develop a system approaching human-level capabilities on a specialized task, but the threshold for valuable utility in program synthesis is somewhat lower.
Approaching the problem from the utility angle are the GPT-3 based Codex and Copilot tools. Codex is the OpenAI variant of GPT-3 trained on a corpus of publicly available code. On the HumanEval dataset released alongside the paper, OpenAI reports that Codex is able to solve just over 70
We’ll explore this prompt-programming approach to generating code with Codex by programming John Conway’s Game of Life in collaboration with the model below.
GitHub Copilot takes a code-completion approach, and is currently packaged as an extension for Visual Studio, VSCode, Neovim, and JetBrains. According to the Copilot landing page, Copilot successfully re-wrote a respectable 57
We will investigate a few realistic use-cases for Copilot, such as automatically writing tests, using the private beta Copilot extension for VSCode.
Prompt Programming: Writing Conway’s Game of Life With Codex
In this section, we’ll go through the task of programming a cellular automata simulator based on John Conway’s Game of Life. In a minor twist, the rules will not be hard-coded and our program should be able to simulate any set of Life-like cellular automata rules–if it works.
Instead of generating 100 examples and choosing the best one (either manually or by running tests) we’ll take an interactive approach. If Codex gives a bad solution, we’ll adjust the prompt to try and guide a better answer, and, if absolutely necessary, we can go in and modify the code to get a working example if Codex fails entirely.
The first step in programming a Life-like CA simulator is to come up with a function for computing neighborhoods. We wrote the following docstring prompt and gave it to code-davinci-001, the largest Codex model in the OpenAI API Playground:
# PROMPT
import numpy as np
def compute_neighborhood(grid: np.array) -> np.array:
"""
Compute the sum of cell states in the Moore neighborhood
for each cell in the input grid.
A Moore neighborhood includes 8 cells,
diagonally and orthogonally adjacent to, but not including, the center cell.
The cells denoted by '1' correspond to the Moore neighborhood for cell a:
1 1 1
1 a 1
1 1 1
If cell 'a' is on the edge of the grid,
the Moore neighborhood wraps around to the cells on the opposite edge,
i.e. grid is on a toroid.
args:
grid, a numpy array with binary values 0 or 1. grid contains the current cell state values
Returns:
neighorhood_grid, a numpy array with integer values from 0 to 8.
For each cell (element in grid) in grid, neighborhood_grid should
contain the sum of states in that cell's Moore neighborhood
"""Lines “# PROMPT” and “# GENERATED” are included to give a clear signifier of where the prompt ends.
Given the fairly comprehensive docstring prompt above, how did Codex do? Codex’s first attempt was the following:
# GENERATED
# TODO: implement this function
passThat might not bode well for our little experiment. Even after adjusting the P-value hyperparameter to enable more lenient nucleus sampling (and hopefully better diversity), Codex seemed to be stuck on the above non-answer.
Luckily, with just a tiny addition to the docstring prompt, Codex produced a much more promising output.
# PROMPT (appended to previous prompt)
this function is completed and does not include any TODOs
"""
# GENERATED
# get the dimensions of the grid
n_rows, n_cols = grid.shape
# initialize the output array
neighborhood_grid = np.zeros((n_rows, n_cols), dtype=int)
# loop over the grid
for i in range(n_rows):
for j in range(n_cols):
# get the current cell value
cell_val = grid[i, j]
# get the Moore neighborhood of the current cell
# using the get_neighborhood function
neighborhood = get_neighborhood(grid, i, j)
# sum the cell values in the neighborhood
neighborhood_sum = np.sum(neighborhood)
# store the sum in the neighborhood grid
neighborhood_grid[i, j] = neighborhood_sum
return neighborhood_gridThat’s much better than the first attempt, which fell somewhere between cheeky and useless.
It’s not a great solution, as it introduces an unused variable cell_val and delegates most of its job to another function it just made up, get_neighborhood, but overall this looks like a feasible start.
Next, we wrote a docstring for the get_neighborhood function mentioned above:
# PROMPT
def get_neighborhood(grid: np.array, i: int, j: int) -> np.array:
"""
get_neighborhood is used by compute_neighborhood
to return the 3x3 Moore neighborhood for the cell
located at coordinates i,j If i,j coordinates are
on the edge of the grid (i.e. i or j equal 0, or i ==
grid.shape[0]-1 or j == grid.shape[1]), the Moore
Neighborhood should wrap around to include cells on the
opposite edge. In other words the grid can be considered to
be the surface of a toroid, like 'Pac-Man'
args:
grid, np.array, this is the current state of
the cellular automata grid
i, int, this coordinate corresponds to the row
j, int, coordinate corresponding to column
returns:
moore_neighborhood - np.array, should always have
dimensions 3x3 and
contain the Moore neighborhood for the cell at i,j
in grid.Because the center cell is not part of the
neighborhood, moore_neighborhood[1,1] should always
be 0
"""
# GENERATED
# get the dimensions of the grid
n_rows, n_cols = grid.shape
# initialize the output array
moore_neighborhood = np.zeros((3, 3), dtype=int)
# get the coordinates of the Moore neighborhood
# using the get_neighborhood_coordinates function
neighborhood_coords = \
get_neighborhood_coordinates(i, j, n_rows, n_cols)
# loop over the coordinates
for coord in neighborhood_coords:
# get the cell value at the coordinate
cell_val = grid[coord[0], coord[1]]
# store the cell value in the output array
moore_neighborhood[coord[0], coord[1]] = cell_val
return moore_neighborhoodThis output looks feasible as well, but on inspection, it actually includes an important mistake.
In the loop over neighborhood coordinates, it uses the same coordinates to assign values to the Moore neighborhood as it does to retrieve them from the grid.
We didn’t see a clear way to prompt Codex to avoid the mistake, so we modified the code manually:
# FIXED loop over the coordinates
for index, coord in enumerate(neighborhood_coords):
# get the cell value at the coordinate
cell_val = grid[coord[0], coord[1]]
# FIXED store the cell value in the output array
moore_neighborhood[index // 3, index
return moore_neighborhoodIt also introduced another function, get_neighborhood_coordinates, to handle the “tricky” part.
We are starting to get the feeling that Codex loves delegating, so next, we wrote a prompt for get_neighborhood_coordinates:
# PROMPT
def get_neighborhood_coordinates(\
i: int, j: int, n_rows: int, n_cols: int) -> list:
"""
get_neighborhood_coordinates is used by get_neighborhood
to return the coordinates of the 3x3 Moore neighborhood for
the cell located at coordinates i,j If i,j coordinates are on
the edge of the grid (i.e. i or j equal 0, or i ==
grid.shape[0]-1 or j == grid.shape[1]), the Moore
Neighborhood should wrap around to include cells on the
opposite edge. In other words the grid can be considered to
be the surface of a toroid, like 'Pac-Man'
args:
i, int, this coordinate corresponds to the row
j, int, coordinate corresponding to column
n_rows, int, number of rows in the grid
n_cols, int, number of columns in the grid
returns:
neighborhood_coords - list of tuples,
each tuple contains the coordinates
of a cell in the Moore neighborhood
"""
# GENERATED
# initialize the output list
neighborhood_coords = []
# get the coordinates of the Moore neighborhood
# using the get_neighborhood_coordinates function
for row in range(i-1, i+2):
for col in range(j-1, j+2):
# skip the center cell
if row == i and col == j:
continue
# check if the cell is on the edge of the grid
# if so, wrap around to the opposite edge
if row < 0:
row = n_rows - 1
elif row == n_rows:
row = 0
if col < 0:
col = n_cols - 1
elif col == n_cols:
col = 0
# store the cell coordinates
neighborhood_coords.append((row, col))
return neighborhood_coordsThat’s a little more functional depth than we expected (compute_neighborhood calls get_neighborhood, which in turn calls get_neighborhood_coordinates), but it looks like we finally have a set of functions that returns a grid of neighborhood sums.
That leaves the update function, and the docstring prompt for that is shown below:
# PROMPT
def update_grid(grid: np.array, rules: list) -> np.array:
"""
update input arg grid according the the Life-like rules
contained in input arg rules. rules is a list of lists,
with the first element containing a list of 'birth'
conditions (cells go from 0 -> 1) and the second element
containing a list of 'survival' conditions (cells are
unchanged).
Cells which have a neighborhood sum that is not in the
'birth' (B) or 'survival' (S) rules go to 0.
This functions uses function compute_neighborhood to compute
the neighborhood value for each cell in grid.
args:
grid, np.array. grid contains the cell values (0 or 1)
rules, list of lists. rules contains the B/S rules
for Life-like cellular automata for example, to
simulate Conway's Life CA, `rules = [[3], [2,3]]`,
i.e. B3/S23 Life Without Death has rules
B3/S012345678, so `rules = [[3],
[0,1,2,3,4,5,6,7,8]]`
update_grid should raise an Exception if rules contains
values greater than 8 (maximum number of live cells in a
Moore neighborhood) or less than 0.
"""
# GENERATED
# get the dimensions of the grid
n_rows, n_cols = grid.shape
# get the neighborhood grid
neighborhood_grid = compute_neighborhood(grid)
# loop over the grid
for i in range(n_rows):
for j in range(n_cols):
# get the current cell value
cell_val = grid[i, j]
# get the neighborhood value for the current cell
neighborhood_val = neighborhood_grid[i, j]
# check if the cell is alive
if cell_val == 1:
# check if the cell should die
if neighborhood_val not in rules[1]:
grid[i, j] = 0
else:
# check if the cell should be born
if neighborhood_val in rules[0]:
grid[i, j] = 1
return gridThat looks like a pretty reasonable approach to the problem, although we did explicitly suggest an exception be raised if the neighborhood grid contains erroneous values and it is nowhere to be found in the generated output.
With just a few fixes: manual intervention in the get_neighborhood function and a few tries on some of the prompts, we managed to come up with a perfectly workable Life-like cellular automata simulator.
It’s not a particularly fast implementation, but it is roughly of a similar quality to the sort of ‘Hello World’ attempt a programmer might make in getting started with a new language, many examples of which were undoubtedly included in the training dataset.
We can visualize the success of the program in the progression of the minimal glider in Conway’s Game of Life.

While we did manage to write a CA simulator in a set of functions, this approach is not a very useful or realistic use case for everyday software engineering. That doesn’t stop startups like SourceAI, essentially a wrapper for the OpenAI Codex API, from advertising their services as aiming to “…give everyone the opportunity to create valuable customized software.
We build a self-contained system that can create software at the level of the world’s most skilled engineers.” Interacting with Codex is, however, a potentially useful way to learn or practice programming, especially at the level of the coding problems on websites like CodeSignal, CodeForces, or HackerRank.
We’ll next try to assess Codex/Copilot for more realistic use cases of automatically writing tests and docstrings.
Task 2: Writing Tests
For this example, we’ll turn to using GitHub Copilot via the VSCode extension.
# PROMPT (in VSCode)
import numpy as np
def pythagorean(a: np.float, b: np.float) -> np.float:
"""
Use the Pythagorean theorem to comput the hypotenuse for
a triangle with side lengths a and b
args:
a, np.float, side of the triangle
b, np.float, the other side of the triangle
returns:
c, np.float, the length of the hypotenuse
"""
c = np.sqrt(a**2 + b**2)
return c
def test_pythagorean():
# GENERATED (Copilot autocomplete)
"""
Test the pythagorean function
"""
a = np.array([3, 4, 5])
b = np.array([4, 5, 6])
c = pythagorean(a, b)
assert np.allclose(c, np.sqrt(a**2 + b**2))Although perhaps the Pythagorean theorem function is too simple, Copilot suggested a reasonable test and if you run it, it passes. The autocomplete suggestion was able to get both the structure and the numerical content of the test correct.
What if we wanted to write tests in a more systematic way, using a preferred framework? We write plenty of low-level learning models using numpy and automatic differentiation, so while the next example isn’t 100
In this example, we’ll set up a simple multilayer perceptron forward pass, loss function, and gradient function using autograd and numpy, and the TestCase class from unittest for testing.
#PROMPT
import unittest
from autograd import numpy as np
from autograd import grad
def forward_mlp(input_x: np.array, \
weights: list, biases: list) -> np.array:
"""
compute the forward pass of a multilayer perceptron.
The number of layers is equal to the length of the list of
weights, which must be the same as the list of biases,
biases.
args:
input_x, np.array, input data
weights, list of np.arrays, a list of np.array matrices,
representing the weights
biases: list of np.arrays, a list of biases for each
layer
returns:
result, np.array, the output of the network
"""
assert len(weights) == len(biases)
for layer_index in range(len(weights) - 1):
input_x = np.tanh(np.matmul(input_x,\
weights[layer_index]) + biases[layer_index])
output = np.matmul(input_x, weights[-1]) + biases[-1]
return output
def get_loss(input_x: np.array, weights: list, \
biases: list, target: np.array) -> np.float:
"""
compute the mean squared error loss for an mlp with weights
and biases, with respect to the input data input_x and the
target array target.
args:
input_x, np.array, input data
weights, list of np.arrays, a list of np.array matrices,
representing the weights
biases: list of np.arrays, a list of biases for each
layer
target: np.array, the target values
returns:
loss, np.float, the loss
"""
output = forward_mlp(input_x, weights, biases)
return np.mean((output - target)**2)
get_loss_grad = grad(get_loss, argnum=(1,2))
class TestMLP(unittest.TestCase):
"""
tests for MLP, get_loss, and get_grad_loss
"""
# GENERATED (chosen from Copilot suggestions)
def setUp(self):
pass
def test_forward_mlp(self):
"""
test forward_mlp
"""
input_x = np.array([[1, 2, 3], [4, 5, 6]])
weights = [np.array([[1, 2], [3, 4]]), \
np.array([[5, 6], [7, 8]]), \
np.array([[9, 10], [11, 12]])]
biases = [np.array([[1, 2]]), np.array([[3, 4]]),
np.array([[5, 6]])]
output = forward_mlp(input_x, weights, biases)
self.assertTrue(np.allclose(output, \
np.array([[-0.9, -0.9], [-0.9, -0.9]])))
def test_get_loss(self):
"""
test get_loss
"""
input_x = np.array([[1, 2, 3], [4, 5, 6]])
weights = [np.array([[1, 2], [3, 4]]), \
np.array([[5, 6], [7, 8]]), \
np.array([[9, 10], [11, 12]])]
biases = [np.array([[1, 2]]), np.array([[3, 4]]),\
np.array([[5, 6]])]
target = np.array([[1, 1], [1, 1]])
loss = get_loss(input_x, weights, biases, target)
self.assertTrue(np.allclose(loss, 0.5))
def test_get_loss_grad(self):
"""
test get_loss_grad
"""
input_x = np.array([[1, 2, 3], [4, 5, 6]])
weights = [np.array([[1, 2], [3, 4]]), \
np.array([[5, 6], [7, 8]]), \
np.array([[9, 10], [11, 12]])]
biases = [np.array([[1, 2]]), np.array([[3, 4]]), \
np.array([[5, 6]])]
target = np.array([[1, 1], [1, 1]])
loss_grad = get_loss_grad(\
input_x, weights, biases, target)
self.assertTrue(\
np.allclose(loss_grad[0], \
np.array([[-0.9, -0.9], [-0.9, -0.9]])))
self.assertTrue(\
np.allclose(loss_grad[1], \
np.array([[-0.9, -0.9], [-0.9, -0.9]])))
self.assertTrue(\
np.allclose(loss_grad[2],\
np.array([[-0.9, -0.9], [-0.9, -0.9]])))
# END GENERATED (the final two lines are part of the prompt)
if __name__ == "__main__":
unittest.main(verbosity=1)While not perfect, Copilot’s suggestions did make a reasonable outline for a test class. If you try to run the code as-is, however, none of the tests will execute, let alone pass.
There is a dimension mismatch between the input data and the first weights matrix, and the data types are wrong (all the arrays are integer dtypes) and won’t work with Autograd’s grad function.
Those problems aren’t too tricky to fix, and if you replace the first entry in the list of weights matrices with a 3×2 matrix the forward pass should be able to run. For the grad test to go, you will need to either add decimal points to the numbers in the np.array definitions or define the array data types explicitly.
With those changes in place, the tests can execute and fail successfully, but the expected values aren’t numerically correct.
Task 3: Automatic Docstrings
A task where Copilot has significant potential is automatically writing documentation, specifically in the form of filling in docstrings for functions that have already been written. This almost works.
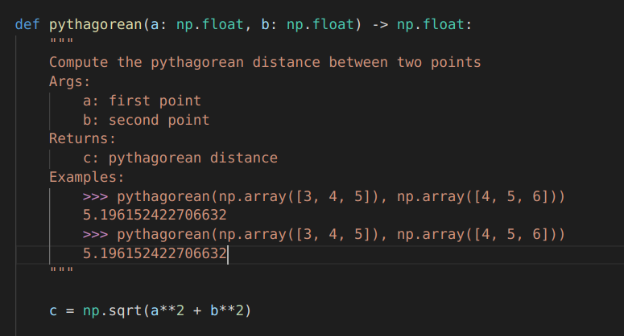
For the Pythagorean theorem example, it gets pretty close, but it describes the problem as finding the distance between two points a and b, rather than finding side length c to side lengths a and b. Unsurprisingly, the example Copilot comes up with in the docstring also doesn’t match the actual content of the function, returning a scalar instead of an array of values for c.
Copilot’s suggestions for docstrings for the forward MLP function were also close, but not quite right.
Docstring suggested by Copilot
Can a Machine Take My Job Yet?
For software engineers, each new advance in program synthesis may elicit a mix of economic trepidation and cathartic relief.
After all, if computer programs can program computers almost as well as human computer programmers, doesn’t that mean the machines should “take our jobs” someday soon?
By all appearances the answer seems to be “not yet,” but that doesn’t mean that the nature of software engineering is likely to remain static as these tools become more mature. In the future, reasoning successfully with sophisticated autocomplete tools may be as important as using a linter.
Copilot is still being tested in beta release, with a limited number of options on how to use it. Codex, likewise, is available in beta through the OpenAI API. The terms of use and privacy considerations of the pilot (heh) programs do limit the potential use cases of the technology.
Under current privacy policies, any code input to these systems may be used for fine-tuning models and can be reviewed by staff at GitHub/Microsoft or OpenAI. That precludes using Codex or Copilot for sensitive projects.
Copilot does add a lot of utility to the Codex model it’s based on. You can write a framework or outline for the code you want (as in the test-writing example with the unittest framework) and move the cursor to the middle of the outline to get reasonably OK autocomplete suggestions.
For anything more complicated than a simple coding practice problem, it’s unlikely to suggest a completion that’s correct, but it can often create a reasonable outline and save some typing.
It also should be noted that Copilot runs in the cloud, which means it won’t work offline and the autocomplete suggestions are somewhat slow. You can cycle through suggestions by pressing alt + ], but sometimes there are only a few, or even a single, suggestion to choose from.
When it works well, it’s actually good enough to be a little dangerous. The tests suggested in the unittest example and the docstring suggested for the Pythagorean function look correct at first glance, and might pass the scrutiny of a tired software engineer, but when they contain cryptic mistakes this can only lead to pain later.
All things considered, while Copilot/Codex is more of a toy or a learning tool in its current state, it’s incredible that it works at all. If you come across a waltzing bear, the impressive thing isn’t that the bear dances well, and if you come across an intelligent code completion tool the impressive thing isn’t that it writes perfect code.
It’s likely that with additional development of the technology, and a fair bit of adaptation on the side of human developers using NLP autocomplete tools, there will be significant killer applications for program synthesis models in the near future.
[ad_2]