Hardy Weinberg’s principle is also known as the Hardy Weinberg equilibrium. Hardy was an English mathematician and Weinberg was a German doctor. Both of them worked separately, to find the principle of the population genetics. Now that principle is known as the Hardy Weinberg theorem. According to this principle, the allelic frequencies, are not changed within the population if certain conditions are met or feasible. There are the following conditions for the Hardy Weinberg equilibrium.
- The new mutations do not occur. So, there is no creation of the new alleles.
- There is no chance of any migration to happen. In other words, there is no movement in or out of the population.
- The population is significantly large.
- In the population, the mating occurs randomly. It means that the individuals are not chosen based on their genotype.
Conditions of Hardy Weinberg Principle
There is no phenomenon of natural selection. So, there are equal chances for all the members of the population, to reproduce, and pass their genes to the next generation. By following all of these conditions, the allelic frequency remains the same. Additionally, there is no change in the genotypic frequencies, and they can be expressed in the terms of the allelic frequencies.
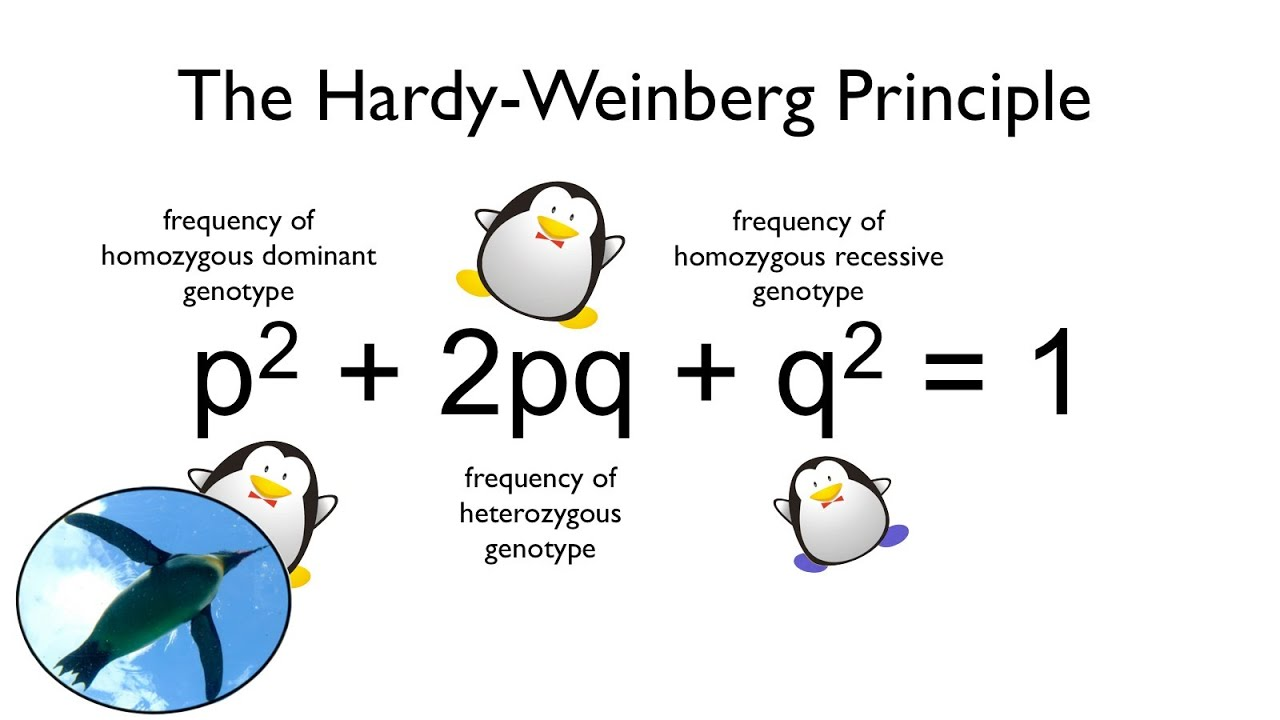
The population geneticist who worked on this principle, represented different alleles as different variables, in their variable models. The variable p represents the frequency of the particular allele. While the variable q is used for representing the frequency of the Y allele. If in the given locus of the population, there are only these two possible alleles, then p + q=1. Generally, it can be said that the p and q alleles, makes all of the alleles for the locus, that is found in the given population. Here the most interesting phenomenon is the frequencies of the resulting genotypes, which is known as the genetic structure of the population, from which the distribution of the phenotypes, can be summarized by the scientists.
Summary of Hardy Weinberg Principle
This principle states that equilibrium is achieved by meeting certain conditions. When equilibrium is established, there is no change in the frequencies of genotypes and alleles. The conditions that should be met are no migration, no mutation, random mating, no natural selection, and the very large size of the population. This principle gives the mathematical baseline to the scientists, for the non-evolving populations, which can be then compared to the evolving populations. If the frequencies of the genotypes or the alleles deviate from the Hardy Weinberg equation, then it is an evolving population.