Applications in finding the area under simple curves, especially lines, circles/parabolas/ellipses (in standard form only)
How do we find areas under a curve, but above the x-axis?
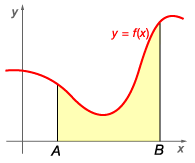
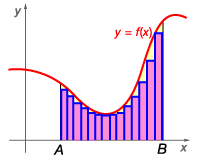
As the number of rectangles used to approximate the area of the region increases, the approximation becomes more accurate.It is possible to find the exact area by letting the
width of each rectangle approach zero. Doing this generates an infinite number of rectangles.
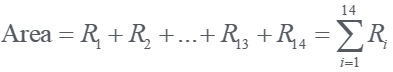
Area = sum of the area of rectangles: the sum of (HXB) is

The definite integral of f from a to b is the limit of the Riemann sum as the lengths of the subintervals approach zero.
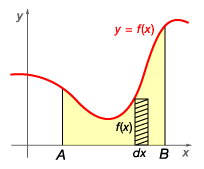
$Area=\int_{A}^{B}{f(x0 dx}=F(B)-F(A)$
All continuous functions are integrable. This means that if a function f is continuous on a closed interval [a,b], then the definite integral over [a,b] exists . A line, parabola, circle and ellipse are all integrable functions.
Line: Consider the line f(x) = x. Find the area between the graph of f and the x-axis on the interval [0, 3].
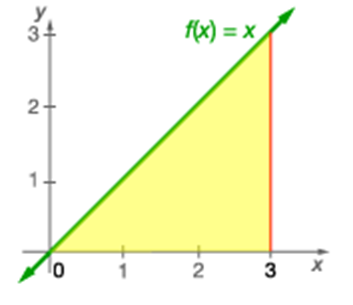
Area = ½ width X height or
$\int_{0}^{3}{x dx}=\lbrack \frac{x^{2}}{2}\rbrack _{0}^{3}$
The square brackets tell you to evaluate the expression at 3 and subtract the value of the expression at 0.
Area = 9/2 units
Example:
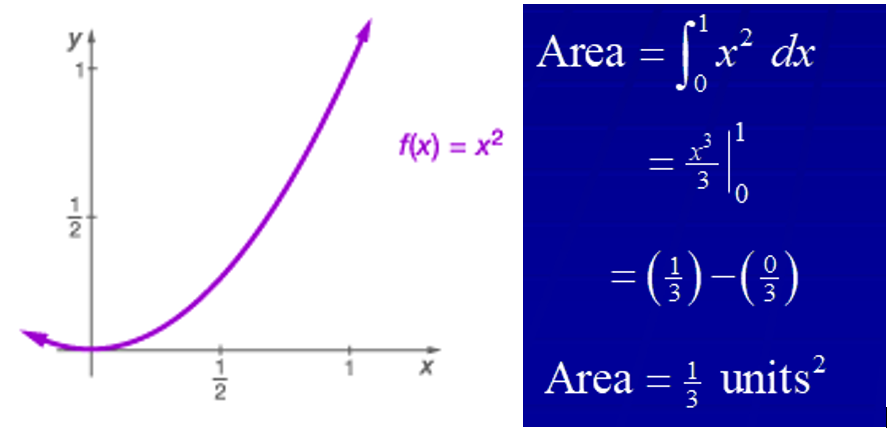
Parabola: Consider f(x) = x2, Find the area between the graph of f and the x-axis on the interval [0, 1].
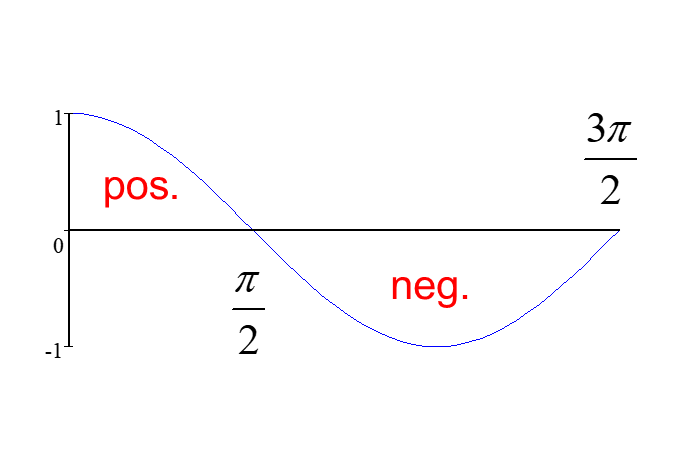
Example: Find the area between the x-axis and the curve y=cos x from x = 0 to x = 3π/2
Note that, for parts of the curve below the x-axis, the definite integral is negative,
. 
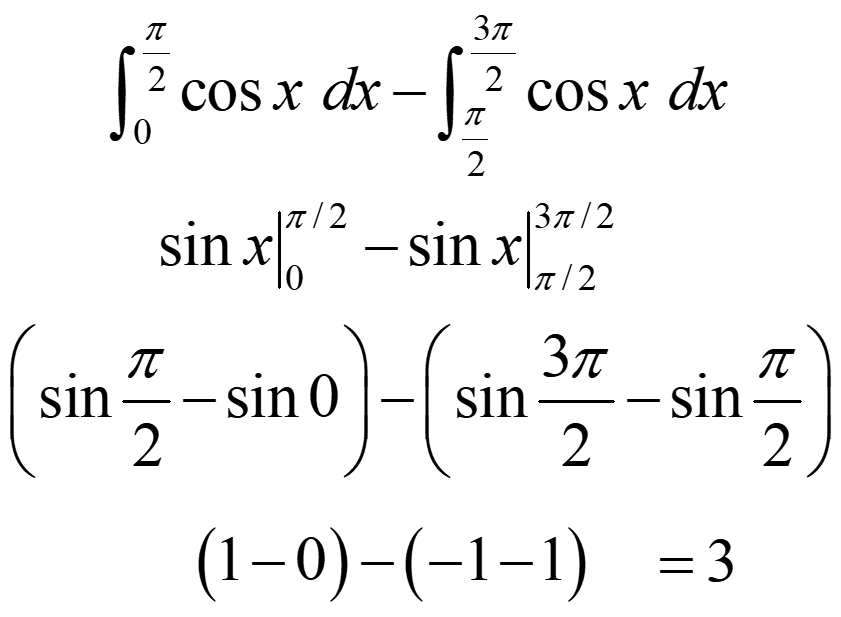
The area bounded by a curve, the y-axis and the lines y = c and y = d is found by switching the xs and ys in the formula.
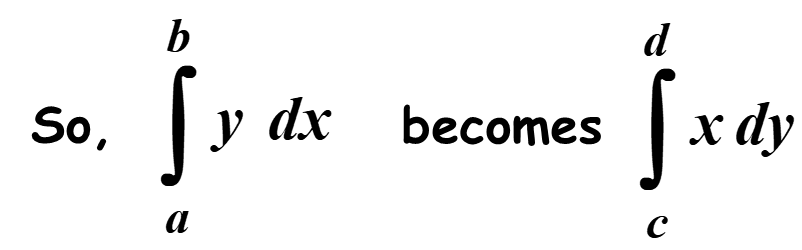
e.g. To find the area between the curve y = √x, the y-axis and the lines y = 1 and y = 2, we need:
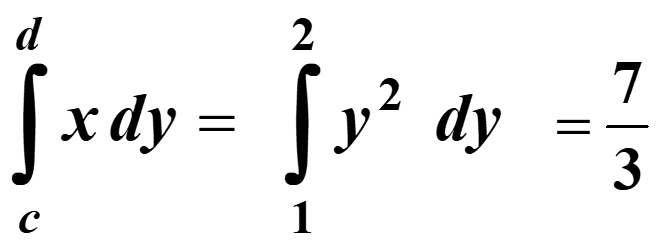
Circle: Consider a circle: x2 +y2 = a2
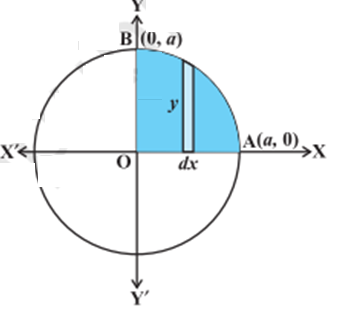
$A=4\int_{0}^{a}{y dx=\int_{0}^{a}{\sqrt{a^{2}-x^{2}}}}$
The circle can be divided into 4 equal sections across the x and y-axis to find the area of a circle. As the region AOBA lies in the 1st quadrant, y is taken as +ive. Integrating, we get:
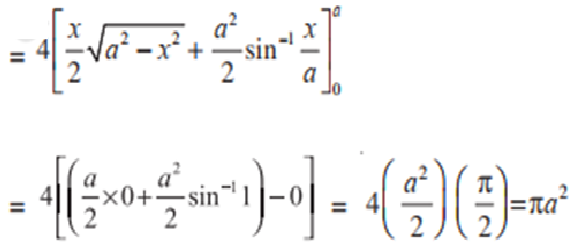
Ellipse: Consider a ellipse:
` 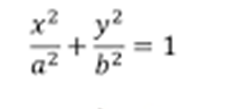
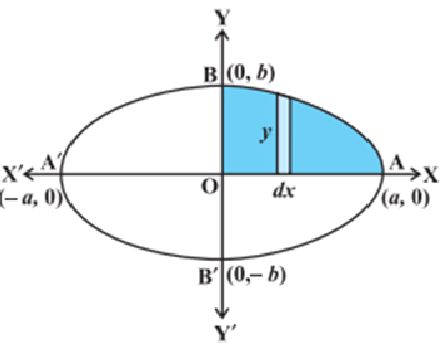
Notice the area of the region AOBA in the first quadrant bounded by the curve, x-axis and the coordinates x = 0, x = a which is ¼ of the area of the complete ellipse.
Take the vertical strip:
$A=4\int_{0}^{a}{y dx }$
$A=4\int_{0}^{a}{\frac{b}{a}\sqrt{a^{2}-x^{2}} dx }$
But the region AOBA lies in the 1st quadrant, y is taken as +ive. So, the required area is
$A=\frac{4b}{a}\lbrack \frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin ^{-1}\frac{x}{a}\rbrack _{0}^{a}$
$A=\frac{4b}{a}\lbrack \frac{a}{2}\sqrt{0}+\frac{a^{2}}{2}\sin ^{-1}1\rbrack -0=\frac{4b}{a}\cdot \frac{a^{2}}{2}\cdot \frac{\pi }{2}=\pi ab$