Introduction to the Binomial Theorem
The Binomial Theorem is known to be the method of an expansion of the algebraic expression that is raised to a finite power extent. The binomial theorem is regarded as a powerful tool for the expansion procedure. It has its significant applications in probability, Algebra, etc.
Binomial Expression: The binomial expression is having 2 dissimilar or not alike terms. For example: x + y, x³ + y³, etc.
Binomial Theorem:
Assuming, n ∈ N, x, y ∈ R therefore,
N in superscript Σ in subscript r=0 ⁿCr xⁿ – r · y^r + ⁿCr xⁿ-r · y^r + …………. + ⁿCn-1 x · yⁿ-1 + ⁿCn · yⁿ
That is, (x + y)ⁿ = ⁿΣr=0 ⁿCr xⁿ-r · y^r
Where,
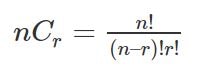
Or,
Description 1: Explanation
Binomial theorem,
The statement of Binomial theorem says that any ‘n’ positive integer, its nth power and the sum of that nth power of the 2 numbers a & b which can be represented as the n + 1 terms’ sum in 
form.
in terms’ sequence, the r index takes up the consecutive values, ranging from 0, 1, 2,…, up to ‘n’. The coefficients are known as the binomial coefficients, which are described by the below formula
Where,
n! = n factorial; It’s the product of 1st ‘n’ natural numbers 1, 2, 3,…, n (& where 0! is described as – equal to 1). Also, the coefficients might present in the series or array, which is oftentimes known as the famous, “Pascal’s Triangle”.
What do you mean by the Binomial Theorem in the context of a positive integral?
The binomial theorem describes the term in (a+b)ⁿ form which can be expressed and expanded in ra^sb^t where s & t components are the non-negative integers which satisfy s + t = n condition. ‘r’ coefficient is known as the positive integer. Also, the terms included are known as the binomial coefficients and the reason because it’s for the positive indices, it extends the plays the role of expansion in the positive powers only.
The general expression for the binomial expansion for any of the indices is given in the form:
(x+y)ⁿ = ⁿC0xⁿyº + ⁿC1x^(n-1)y¹ + ⁿC2x^(n-2)y² + …….. + ⁿC(n-1) x¹y^(n-1) + ⁿCnx0yⁿ.
Properties of the expansion:
you see at a & b powers, then, ‘a’ exponent gets decreased by 1 in the consecutive or successive terms. At the same time, b’s exponent gets increased by 1 in the form of successive terms. Let’s say, in the expansion of:
(a+b)³ = a³+3a²b+3ab²+b³
- Talking of the first term, a³, exponent of a = 3; exponent of b = 0
- Taking the second term, 3a²b, exponent of a = 2; exponent of b = 1
- Taking the third term, 3ab², exponent of a = 1; exponent of b = 2
- Taking the fourth term b3, exponent of a =0; exponent of b is 3
Now, in the expansion, the total no. of terms is 1 more than the index or the component of (a+b). Let’s say, taking the expansion of (a+b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴, so, the index of (a+b) = 4 & in the expansion, the number of terms is equal to 5.
The index or the exponent of (a+b) will be equal to the sum of exponents of a & b in each term of expansion.
We’ll be seeing the relation between the terms’ coefficients and the index (a+b) in the expansion.
Index
Coefficients
&;
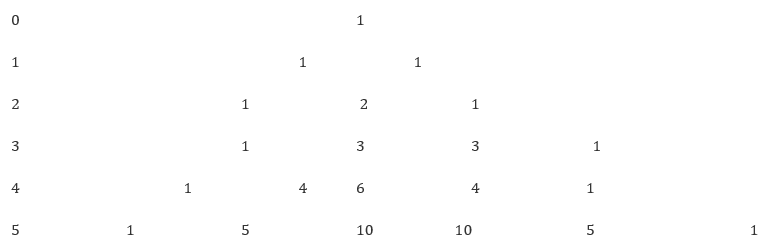
First and the last terms’ coefficients of the expansion (a+b)ⁿ = 1
where n = any integer.
Now with the addition of 1’s of the index
The sum of the 1’s of an index makes up to obtain 2 for index 2.
likewise, on the addition of 1 and 2 of the indexes 2 makes up to get 3’s of the index 3.
In the diagram given below, you’ll have a better understanding of the indexes and coefficients
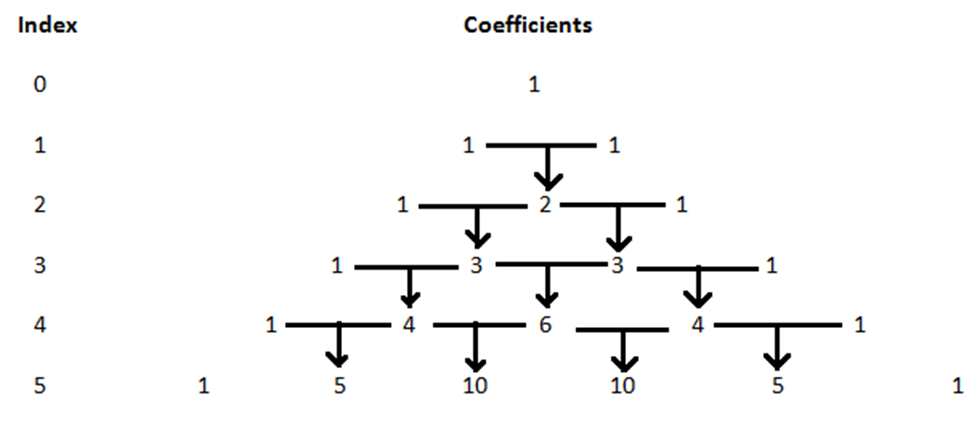
So, the above discussion is summarized binomial theorem introduction for the positive integral indices.