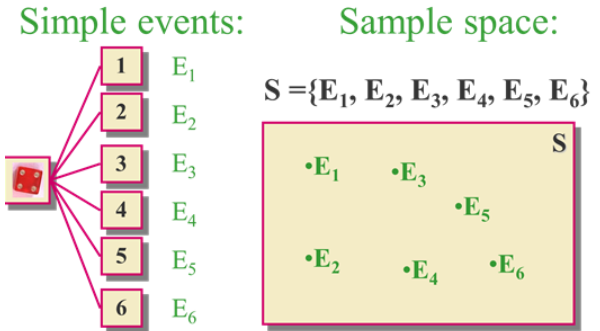
Probability: event
An event is an outcome for any experiment and it is denoted by a capital letter. It is the basic element to which probability is applied. When an experiment is performed, an event either happens, or it doesn’t. A simple event is denoted by a E with a subscript where the event is a collection of simple events. An unusual event has a low probability of occurring.
Die Toss:

The probability of an event A is a term to deduce “how often” A will occur. We write P(A). Suppose that an experiment is performed n times. The relative frequency for an event A is
![]()
If we let n get infinitely large, the equation for probability is as follows:
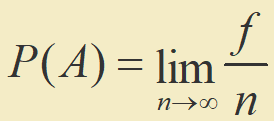
P(A) must be between 0 and 1.b If event A can never occur, P(A) = 0. If event A always occurs, P(A) =1. Also, the sum of the probabilities for all simple events in S equals 1. Hence, the probability of an event A is found by adding the probabilities of all the simple events contained in A. Let A be the event A = {o1, o2, …, ok}, where o1, o2, …, ok are k different outcomes. Then,
![]()
Example: When you toss two coins, find the probability of at least one head from the tosses shall appear.
Answer: At least one head means one head or two heads are possible.
- Step 1: Find the sample space for coin toss:{ HH, HT, TH, TT} There are four possible outcomes.
- Step 2: Find the no. of outcomes of the event to suffice “at least 1 head from two tosses”. Answer: 3 : { HH, HT, TH}
- Step 3: Use P(E)= n(E) / n(S) = ¾ = 0.75 = 75
Example: If tuberculous meningitis had a case fatality of 20
(a) Find the probability that tuberculous meningitis would be fatal in two randomly selected patients (the two events are independent) (b) If two patients are selected randomly what is the probability that at least one of them will die? (a) P(1st die and 2nd die) = 20
(b) P(1st die or 2nd die) = P(1st die) + P(2nd die) – P(both die) = 20
= 36
Example : Find the probability for a randomly chosen month to be January? Answer: If we choose something out of say ‘n’ things, then the number of favourable outcomes is 1 (since we are choosing only one thing) and the number of unfavourable outcomes is equal to the number of the things that we are choosing from. Here we are choosing one month (January) out of a total of twelve months. So the probability of choosing any month including January from 12 months is = 1/12.