You have already known that there is a very little difference between exponential and logarithmic functions. It is however important to recognize the most suitable ways to deal with these.
Now, you may already know that the domain of a function is the set of probable inputs and also known as the x values. Also, that the range of a function is the set of expected output values that may be attained.
Domain and Range of Exponential Function
Let’s consider a simple exponential function as an example $f(x)=2^{x}$ it will have its domain as an entire real line i.e. real numbers. However, its range is supposed to be a set of positive real numbers only. This implies that $y>0$. Also, consider that $f(x)$ would never take up a positive value. Further, it would never actually reach 0. Although it is likely to approach asymptotically as $x$ moves $(-\infty , \infty ).$
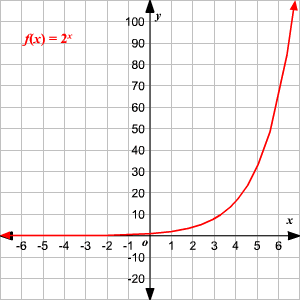
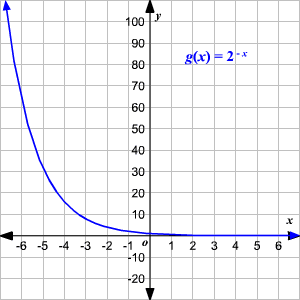
If we replace $x$ with $-x$, we would get an equation like $g(x)=2^{-x}.$ The graph, in this case, would be like the one given below, where it gets reflected around the y-axis but no change is observed in the domain and range.
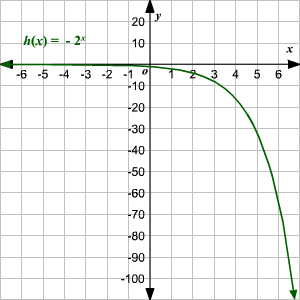
If a negative sign is placed into the equation to obtain something defined as $h(x)=-2^{x};$ the graph then tends to get reflected around the x-axis. We would still have the entire real line as the domain for the function. The range, however, will now have negative numbers which imply that $y<0.$
Now, let’s consider the function $f(x)=(-2)^{x}$. Here, when $x=\frac{1}{2}$ , $y$ should be a complex number. Hence, everything here turns out to be tricky. In order to understand this mechanism perfectly, it would be vital to make sure that these bases are positive to be able to understand it more clearly. It is important to understand things from the perspective of the real-valued world.
Generally, the graph of this basic exponential function $y=a^{x}$ tends to drop from $\infty $ to 0 considering that $0<a<1 $ while $x$ varies from negative infinity $-\infty $ to positive infinity $\infty $ and rises from 0 to $\infty $ when $a>1.$
The exponential function $y=a^{x}$ can be transformed and shifted vertically by $k$ units and horizontally by $h$ units with the equation $y=a^{(x+h)}+k.$ with this, the domain of the function remains unchanged and the range turns to be ${y ∈ R|y>h}$.
With the help of the above description, you would be able to tackle with domain of exponential functions perfectly.