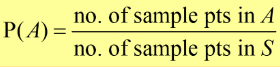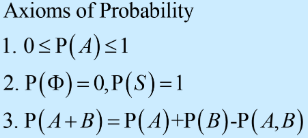Probability: Axiomatic (set theoretic) probability
Given an experiment and a sample space, probability is used to designate each event A a number P(A), called the probability of the event A. This designation provides a precise measure of the chance that A will occur.
To ensure that the probability assignments are consistent with the intuitive notions of probability, all assignments should satisfy the following axiomsof probability. These axioms are the basic properties of a set.
If A is an event and is a subset of S, the sample space, then the following are true:
Axiom 1: For any event A, P(A) ≥ 0 and 0 ≤ P (E) ≤ 1
Axiom 2: P(S) = 1
Axiom 3: If A1, A2, A3,… is an infinite collection of disjoint events, then
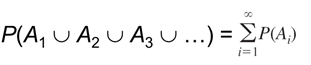
This means that P(φ ) = 0 The probability of an empty set is zero. Consequence: IF P(A ∩ B) = 0 then A ∩ B = φ which implies A and B are mutually exclusive.
Axiom 1 reflects the intuitive notion that the chance of A occurring should be non negative. The sample space is by definition the event that must occur when the experiment is performed ( S contains all possible outcomes), so Axiom 2 says that the maximum possible probability of 1 is assigned to S.The third axiom formalizes the idea that that at least one of a number of events will occur and no two of the events can occur simultaneously. In this case, the chance of at least one occurring is the sum of the chances of the individual events.
From these axioms, more axioms are developed:
Axiom 4: The rule for unions, in general, is P(A U B) = P(A) + P(B) – P(A ∩ B)
Axiom 5: If A and B are mutually exclusive then P(A U B) = P(A) + P(B).
Axiom 6: The rule for complimentary events is P(E’) = 1 – P(E).
For instance, let E be the event of tossing two dice such that the sum of the face is even. Let F be the event that represents the addition of the faces is greater than 9. What is the probability of the sum of the faces that are even and greater than 9? So we need to find P(E ∩ F).
The only rolls that correspond to that event are (6,4), (4,6), (5,5), (6,6).Thus P(E ∩ F)=4/36=1/9.
What is the probability of the sum of the faces to be even greater than 9?
P(E U F)=P(E)+P(F)-P(E ∩ F)=1/2+1/6-1/9=5/9