Definition of trigonometric functions with the help of unit circle
With the use of the unit circle, you can easily define the sine, tangent, and cosine functions.
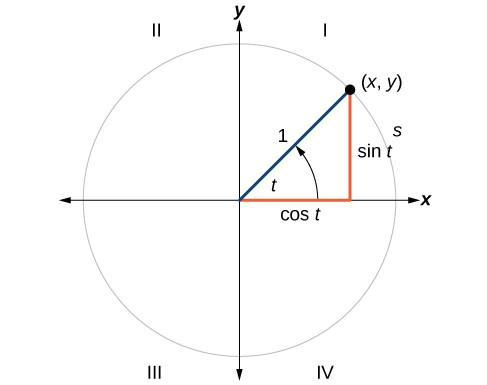
In this part, we’ll be redefining these functions in the context of the unit circle. Recalling that the unit circle is the circle which is centrally positioned at the origin of the circle having radius one. “t” is the angle measured in radians, which forms length’s arc, expressed as ‘s’.
The co-ordinated plane (plus the unit circle) is divided between the two axes which is axis x and the axis y and it’s centrally positioned at the origin. The two-axis x and y is also divided into 4 quarters, known as the quadrants.
The 4 quadrants are given the marks – I, II, III, and IV.
For any t angle, we can mark its side’s intersection plus the unit circle with the help of its coordinates (x,y). The coordinates y and x result as the outputs of the trigonometric functions denoted by f (t) where, f (t) = sin t & f(t)=cost, respectively.
This means that,
x = cos t
y = sin t
The below-given diagram of a unit circle clearly describes these coordinates.
The Trigonometric functions over a unit circle
In consideration of every point of the unit circle, it’s that we want to calculate the accurate length to its projections on x-axis and y-axis from the point of origin.
From the origin point, the length to its projections of a point on axis x is known as the Cosine and the length to point’s projection point from the origin on axis y is known as the Sine.
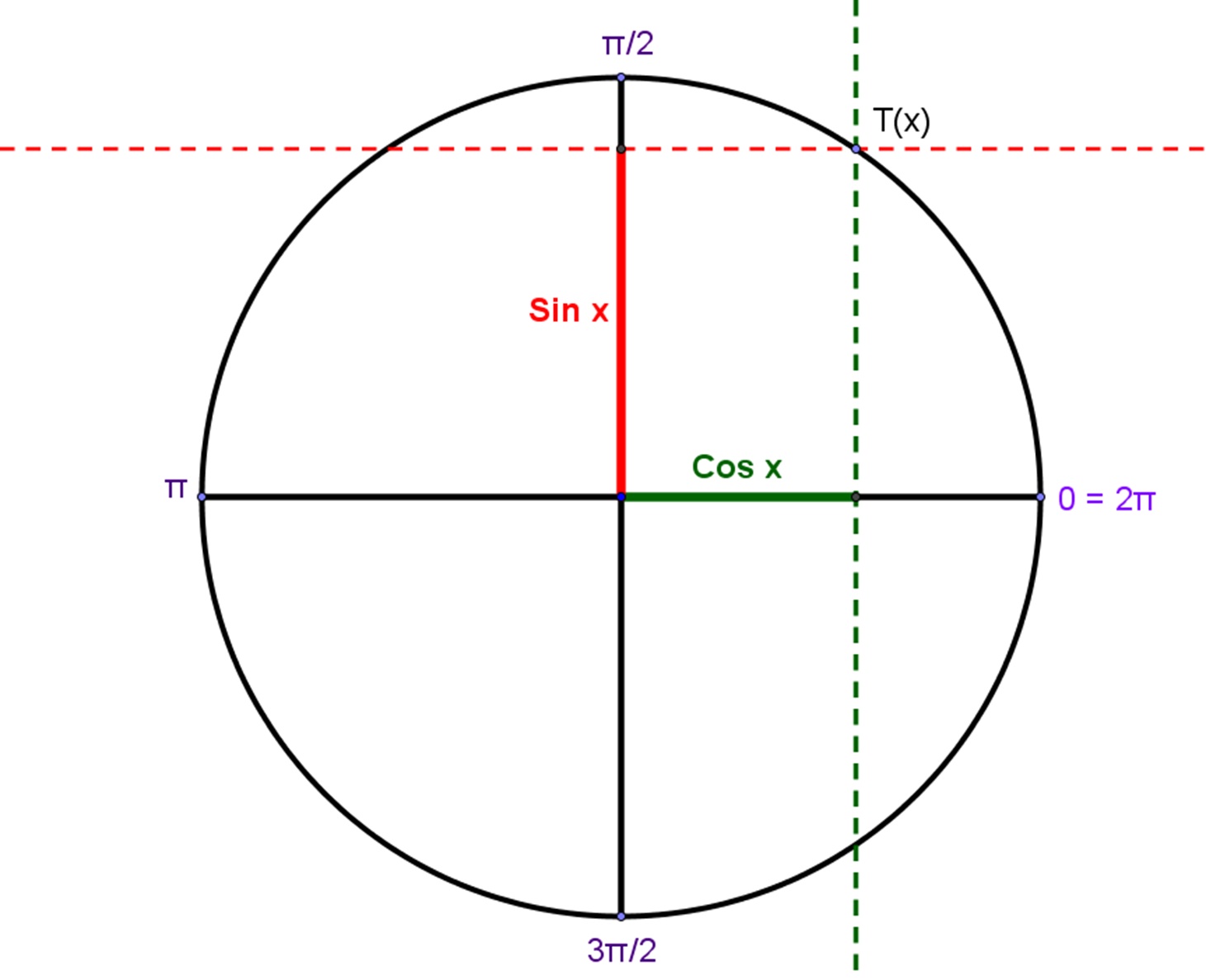
How do you get an angle whose sine plus cosine value you have known? It is very easy to understand. If you’re having a default value of sine then, you will first find that particular value on the y-axis and draw the parallel line from axis x through this point.
You will have 2 points on the unit line, which you will add to the original. 2 angles are the ones whose one arm happens to be those lines plus the second axis x will be those angles which you’re looking for.
If Cosine value is given for the angle, you will simply get the value on the x-axis. From the y-axis, draw a parallel line through that specific point which links the points you received on the unit circle in addition to connecting them with the origin.
The two angles with one arm having those lines and the second are the x-axis that would be the angles whosoever is in search of.
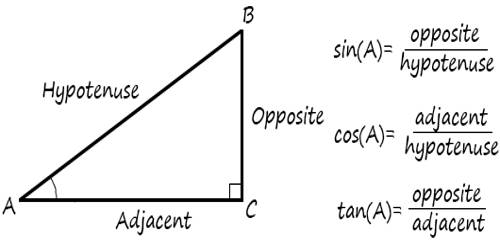
In this,
Adjacent = adjacent side to θ angle
Opposite = opposite side to θ angle
Hypotenuse = Hypotenuse side to θ angle
Sin θ = Opposite / Hypotenuse
Cos θ = Adjacent / Hypotenuse
Tan θ = Opposite / adjacent
Cosec θ = Hypo. / opp.
Cot θ = adj. / opp.
Sec θ = Hypo. / adj.
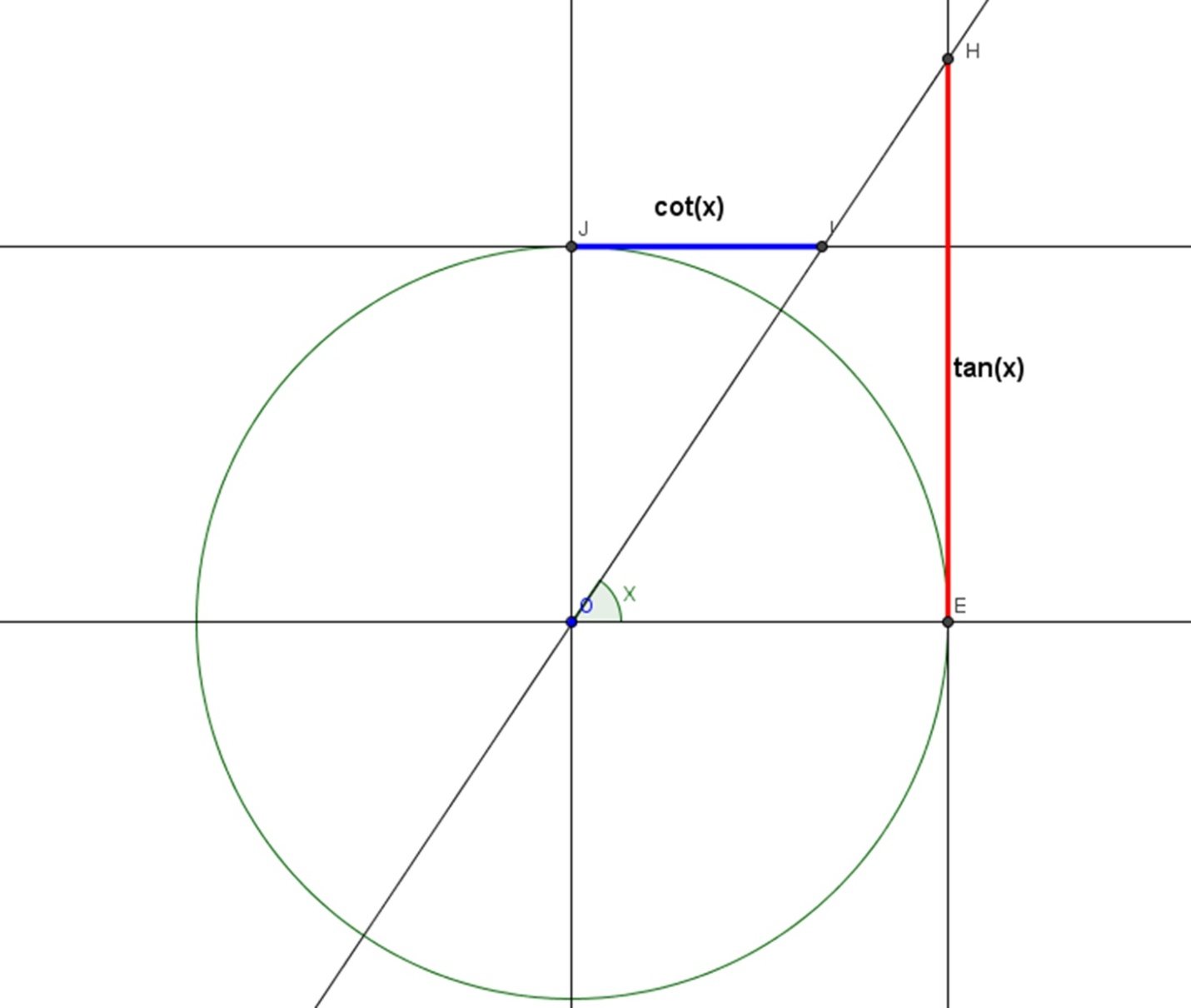
Two more important trigonometric functions are known as the tangent (tan) and the cotangent (cot).
These are the derived functions, however, it’s equally significant to remember.
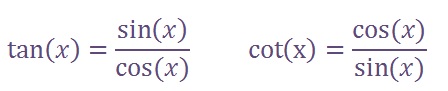
To get tangent value, we first draw a parallel line to the y=axis which passes through the point (1, 0).
To get cotangent value, we first draw a parallel line to the x-axis which passes through the (0, 1) point.
In the next step, we then sketch a line from origin plus a point on the unit line whose value you’re searching for.
You will be getting two intersections:
- First one with a perpendicular line to x – axis
- Another one with a perpendicular line to y – axis.
At the point, the tangent value is equal to the length from the intersection with a perpendicular line to the x-axis and the y-axis.