While dealing with functions and relations, it is quite certain to come across the rules regarding Greatest Integer Function.
What is Greatest Integer Function?
For any real function, the greatest integer function is known to be represented by. This function tends to round off the number down to an integer that is significantly less/smaller than the number. This function is often referred to as the floor function. The greatest integer function, in other words, is a function set such that the output for the same is the greatest integer that is probably equal or greater than the number.
It may, however, get a bit confusing. Consider it the other way; the greatest integer function accepts input and delivers the output based on the following two rules:
- If the input is an integer then the output is most likely to be that integer.
- If the input is not an integer, the output would be the next smallest integer.
Domain and Range of Greatest Integer Function
Recalling the definition of the greatest integer function, it is known to be the real valued function $f:R\to R, y=[x]$ for every $x?R$. For every possible value of $x, f(x)$ takes the greatest integer that is equal to or greater than the value of $x$.
Greatest integer functions are said to be generally defined piecewise, the domain for the same is known to be a series of real numbers that are actually divided into intervals. For example: [-4, 3), [-3, 2), [-2, 1), [-1, 0) which may continue further.
Graphing the Greatest Integer Function
While the intervals had been represented in the form of (n, n+1), the value of the greatest integer function is supposed to be n. Here, n is an integer. Consider the given example, for the interval [3, 4) the greatest integer function would be 3. The graph for this would not be continuous. For instance, consider the graph below for the function $f(x)=[x]$.
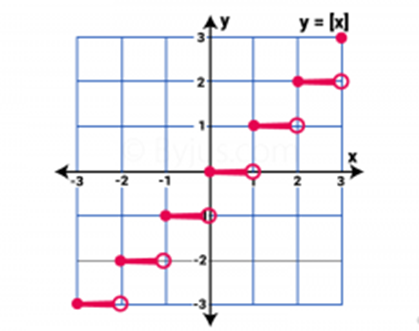
Since the above graph looks much like a group of steps on the plane, the greatest integer functions are often addressed as step functions. In every step, the left end is blocked (with a dark dot) in order to represent that the point is a part of the respective graph. And on the other hand, the right endpoint (represented by open circles), certainly indicates that those points aren’t a part of the graphical representation.
It could be observed from the graph that the function $f(x)$ is the same for every interval. The value of the function therefore stays constant with an interval. For instance, for the interval $[$-5, -4), the value of $f(x)$ would be -5.