Since you may be focusing a better grip on functions and relations, it is absolutely important to take a look at suitable operations with rational functions.
What is a rational function?
A rational function is said to be the one that could be written down as the quotient for two polynomials. For instance, consider a rational function $r(x)=\frac{p(x)}{q(x)}$. , $q(x)$ is not the zero polynomial. This is because, as per the definition, any rational function can have a variable within its denominator. However the domain and range for these rational functions do not really contain all the real numbers.
Domain and Range of Rational Functions
The domain of a considerable function $f(x)$ is known to be a set of values for which the function has been actually defined. Also, the range for $f(x)$ will be the set of values that could be taken up by$ f$. A rational function is known to exist in the form of $(x)=\frac{p(x)}{q(x)}$ . Here $p(x)$ and $q(x)$ are supposed to be polynomials and $q(x)\ne 0$.
The domain of any rational functions is known to comprise of all real numbers $x$. However, this excludes the ones whose denominator is 0. In order to find these $x$ values that need to be excluded from the domain set of the considerable rational function, you would be required to equate the denominator with zero and further solve for$ x$.
For instance, consider a parent function $(x)=\frac{1}{x}$. The domain set for this function consists of all real numbers except $x=0$. Or the function $f(x)=\frac{1}{x-4}$ whose domain set values are all real numbers except $x=4.$
Now, consider another function $f(x)=\frac{(x+1)(x-2)}{(x-2)}. $Once simplified, when $x\ne 2$, it turns out to be a linear function $f(x)=x+1 .$ However, the original function has not been defined at $x=2. $ Therefore, when $x=2$ the graph is left with a hole.
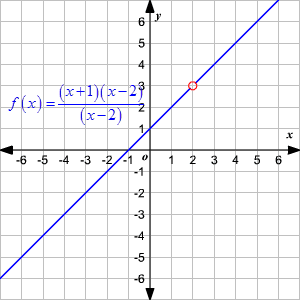
One of the ways to find the range for a rational function could be finding the domain of an inverse function. The most suitable another way to do so would be to sketch out the graph and subsequently identify the range.
Let’s consider the parent function once again, $f(x)=\frac{1}{x}. $ We already know that the function would not be defined when $x=0. $ When $x\to 0, $from either sides of zero, $f(x)\to \infty .$ Similarly, as $x\to \pm \infty , $ $f(x)\to 0.$
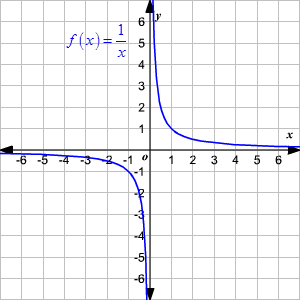
The graph approaches the x-axis while $x$ tends to be negative or positive infinity however never really touches the x-axis. This certainly means that the function could take up all the real values except 0. And therefore, the range of the function is supposed to be a set of real numbers except 0.