Cartesian product is determined by the two words that comprise the same. The word Cartesian is said to be derived from the name of a French Philosopher and mathematician René Descartes. The Cartesian product of any two non empty sets say A and B would be denoted and determined as A x B. Also, it would be defines as a collection of ordered pair (a,b) such that and b∈B and a∈A .
Thus, considering the same,
A×B = { (a,b):a∈A,b∈B }
It could also be called as direct product, cross product or product set of values A and B. Collection of the ordered pairs here is something very important to note. Ordered pairs mean that two elements derived from a set are to be written in a considerable order. In that case if a is not equal to b (a ≠ b), the ordered pairs (b,a) and (a,b) would be distinct.
For an example, consider P as the set of marks in a school form and Q as the set of sections for them. P and Q are therefore, defined as under,
P = {8,9,10}
Q = {A,B,C,D}
In that case, P x Q, according to the stated definition would be,
P x Q= { (8,A) , (8,B) , (8,C) , (8,D) ,(9,A) , (9,B) ,(9,C),(9,D),(10,A),(10,B),(10,c),(10,D)}
There are 12 ordered pairs in total. While n(Q)and n(P) are representing elements in the sets Q and P respectively, then probably, n(Q) =4 and n(P) = 3. Further,
n(P×Q) = 3 × 4 = 12. The same has been depicted in the figure.
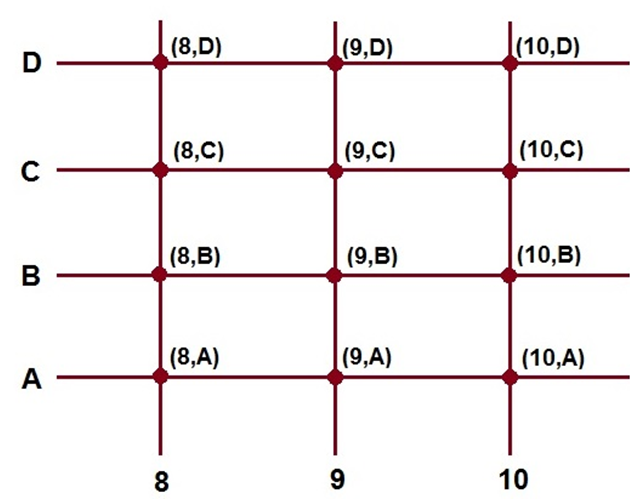
The figure depicts the Cartesian plane, formed by P x Q. Each point on the plane is said to represent an ordered pair which gets its first element from P and the second one from Q. If the number of elements in the sets M and N are, a and b respectively then the number of elements in the Cartesian products of the sets will be ab.
If n(M) = a and n(N) = b and , then n( A × B) = ab.
Two conclusions can be drawn from this property,
- M × N = ϕ (While either one or both the sets are empty).
- M x N would be an infinite set if any one of the sets are known to be infinite.
Cartesian product of sets is not limited to just two sets. Rather it could be held for more than two. However, with an increase in the number of sets the complexity tends to increase.