Equal Sets
When two sets contains same elements, then they are regarded as equal sets; it’s regardless of the fact in which order these elements are arranged. What matters is that these are identical elements are present in each of the sets. So, here a few examples based on equal sets.
Let’s Say:
- {2, 9, 6, 5} & {5, 6, 9, 2}
- { Monkey, Giraffe, Camel, Goat } & { Goat, Giraffe, Monkey, Camel }
Simply, the Equivalent Set refers to a set with elements’ equal number. The set doesn’t have the exact same elements, altogether same elements’ number. Let’s look at a few examples:
Example 1
- Set A: { 1,2,3,4,5 }
- Set B: { Monday, Tuesday, Wednesday, Thursday, Friday }
From the above example, you can see that the set A is comprised of numbers whereas set B is comprised of weekdays. On comparison of both sets, the sets are having an equal number of elements, which is 5. Set A is having numbering from 1 to 5 i.e. in total 5 elements, and Set B is having five days of the week. And this results in the equivalent sets!
The cardinality of Equal Sets
The cardinality of the set refers to n(A)= x, where, “x” element represents elements’ number belonging to set A.
A = { 2, 6, 8, 10, 12 }
B = { f, g, h, i, j, k }
C = { g, h, i }
From above, the conclusion is that the cardinality of set A is 6 and also, the cardinality of set B is 6.
n (A) = n (B) = 6
Therefore, as per the elements’ number or in the context of cardinality, the two sets are known as the equal sets if in the condition,
n(A) = n(B) plus,
Aso, x∈A, x∈B
Then,
A = B
Symbol of Equal Sets

For the representation of the equal sets, “=” symbol is used which is known as equality.
And for the unequal sets, “≠” symbol is used which means it is not equal to.
As from the above example,
A = B i.e. Set A is equal to Set B
But from the above example only, you can easily see that A ≠ C, that is, Set A is not having an equal value to Set C.
Subsets
The Set A is mentioned as a subset of set B if set A’s elements entirely are Set B’s elements too. In other words, you can say that Set A refers to set B’s subset if x is belonging to A means X is also belonging to B.
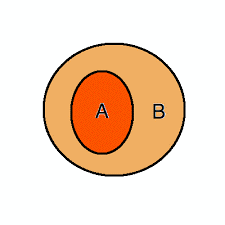
Here, Set A’s all elements are contained in Set B. Therefore, A refers to B’s subset. Also, we from this you can say that B contains A, hence, B exists as a superset of A.
Example:
A = { January, February, March, April, May, June, July }
B = { January, February, March, April }
From the above, all B’s elements are seen in A, therefore, B is a subset of A.
Subset’s Symbol
For subset’s representation, we use “⊆” symbol which means that “It’s a subset of”.
A shown in the above example, B⊆A, that is, B is A’s subset. Considering superset, “ ⊇” symbol is used and that means “is a superset of”.
A ⊇B, that is, A refers to B’s superset, or A contains B’s elements or A contains B.
If X is not Y’s subset then we pen down it with “⊈” Symbol which means “ is not a subset of”.
Writing it as, X⊈Y that means, X is not Y’s subset.
Symbolically,
You can write a subset’s definition as the following
A⊆B if x A x B
The above reads as “A is B’s subset if x belonging to A indicates that x too, is belonging to B.
Proper Subset
If X refers to Y’s subset but, Y is not X’s subset, then, X is known to be Y’s Proper Subset and if all X’s elements exist in Y but all Y’s elements don’t exist in X. Then, X is Y’s proper subset. And Y is X’s proper superset.
“⊂” symbol is denotion for it which means “is a proper subset of”. Whereas, “⊃” means “is a proper superset of”.
Example
Here,
A = { 6, 7, 8, 9, 10 }
B = { 8, 9, 10}
It depicts that B’s all elements are A’s all elements, with that in addition, A’s all elements are not present in B. Therefore, B⊂A that is, B is A’s proper subset.