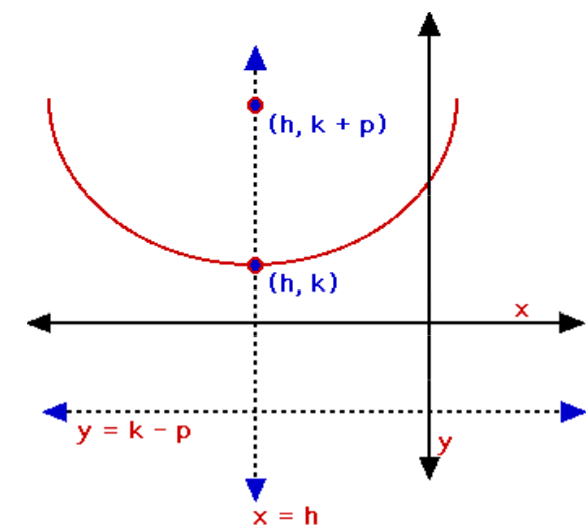
For a parabola with the axis of symmetry parallel to the y-axis and vertex at (h, k), the standard form is
(x – h)2 = 4p(y – k)
Example 1: Find the equation of the parabola that has a minimum at(-2, 6) and passes through the point (2, 8).
The axis of symmetry is parallel to the y-axis.The vertex is (-2, 6), therefore, h = -2 and k = 6.Substitute into the standard form of the equation and solve for p: x = 2 and y = 8
![]()
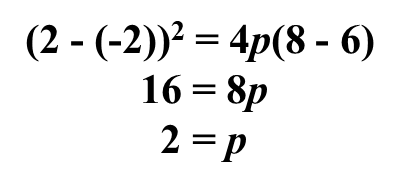
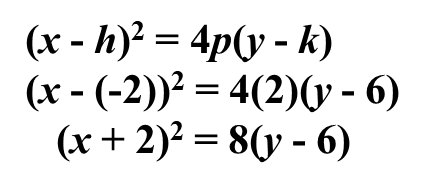
The equation of the axis of symmetry is x = h and coordinates of the focus are (h, k + p). This means that the equation of the directrix can be written as y = k – p. When p is positive, the parabola opens upward.When p is negative, the parabola opens downward.
For a parabola with an axis of symmetry parallel to the x-axis and a vertex at (h, k), the standard form is:
(y – k)2 = 4p(x – h)
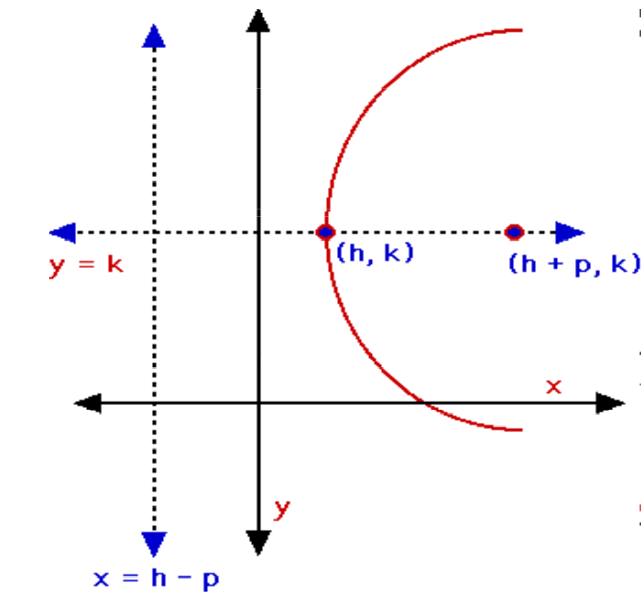
The equation of the axis of symmetry is y = k and the coordinates of the focus are (h + p, k). This means that the equation of the directrix can be written as x = h – p.When p is positive, the parabola opens to the right and when p is negative, the parabola opens to the left.
Example 2: Write the equation of the parabola with a focus at (3, 5) and the directrix at x = 9, in standard form and general form.
The distance from the focus to the directrix is 6 units, therefore, 2p = -6, p = -3. Thus, the vertex is (6, 5). The axis of symmetry is parallel to the x-axis:h = 6 and k = 5
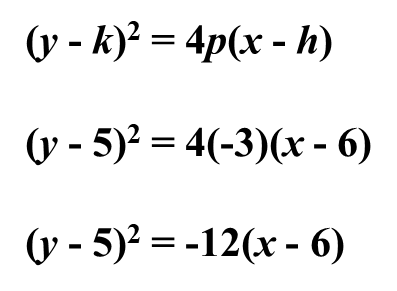
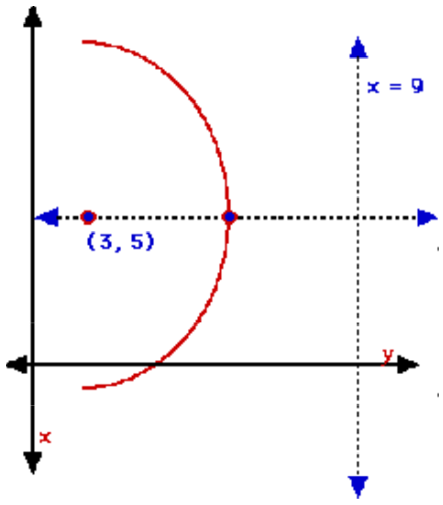
Example 3. Find the coordinates of the vertex and focus, the equation of the directrix, the axis of symmetry, and the direction of opening of 2x2 + 4x – 2y + 6 = 0.
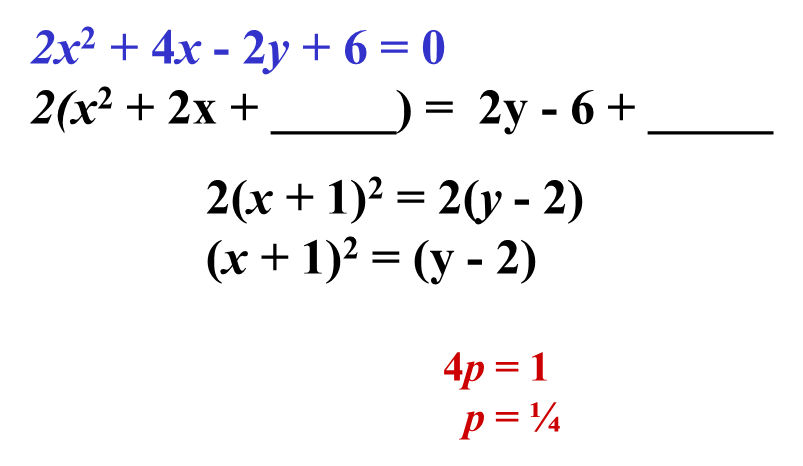
The parabola opens to upward. The vertex is (-1, 2). The focus is ( -1, 2 ¼ ). The Equation of directrix is y = 1¾ .Notice that the axis of symmetry is x = -1 .
The general form of any parabola is written as:
Where either A or B is zero. Also, the “Completing the Square” method can be used to convert the General Form to Standard Form.
