Probability: random experiments – sample spaces
The sample space, S, for a random phenomenon is defined as the set of all possible outcomes. It is basically a list of unique, non-overlapping possible outcomes of random circumstances shown in a set representation denoted by symbol ‘S’. The outcomes must be mutually exclusive and exhaustive from each other. Mutually exclusive is a term used to explain that the outcomes are distinct and non-overlapping from each other and exhaustive is a term that means complete.
Each of the outcomes in a random experiment is referred to as a sample point. For an experiment containing n sample points, label namelyE1, E2, E3, … ,En: the sample space of an experiment is the set of all sample points which can be written as S = {E1, E2, E3, … ,En}.
The sample space S may contain any of the following characteristics:
- A finite number of countable outcomes.
- A countably, however infinite number of outcomes, or
- An uncountably infinite number of outcomes that are unpredictable.
A countably infinite number of outcomes contains outcomes that occur in a one to one correspondence with the positive integers
{1, 2, 3, 4, 5, …}
This means that the outcomes can be labelled with the positive integers as shown below.
S = {O1, O2, O3, O4, O5, …}
An uncountably infinite number of outcomes means that the outcomes are possible to be arranged in a one to one correspondence with the positive integers.
For a set of two families of outcomes S = {(x, y)}. In this case, x is the family of outcomes selected from the first draw and y is the family selected on the second draw. S represents the concise description of a large sample space.
P ( Sample space) = 1
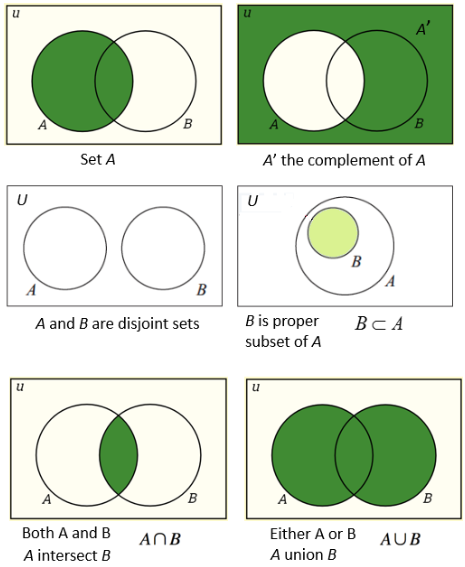
Set Operations and Venn Diagrams
Example: A spinner on a circular disc shown below is spun and points at a value x on a circular disc whose circumference is 1.
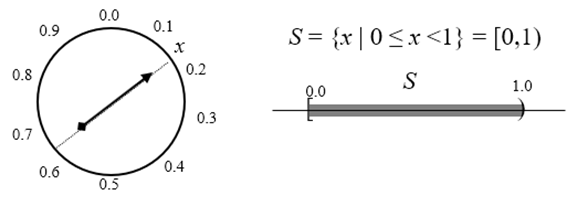
Example: Flip one unbiased coin (n = 2). S = {H, T}, where the symbols representing H = head, and T= tail.
P(H) = 1/2 = 0.50 and P(T) = 1/2 = 0.50.
P(H) + P(T) = 0.50 + 0.50 = 1.
Example: Tossing two coins – outcomes S ={Head, Tail}
outcome (x, y), x = value showing on die 1 and y = value showing on die 2
S = {(H, H), (H, T), (T, T), T, H)}
Example: Rolling a die – outcomes
![]()
= {1, 2, 3, 4, 5, 6}
Rolling two balanced dice – 36 outcomes