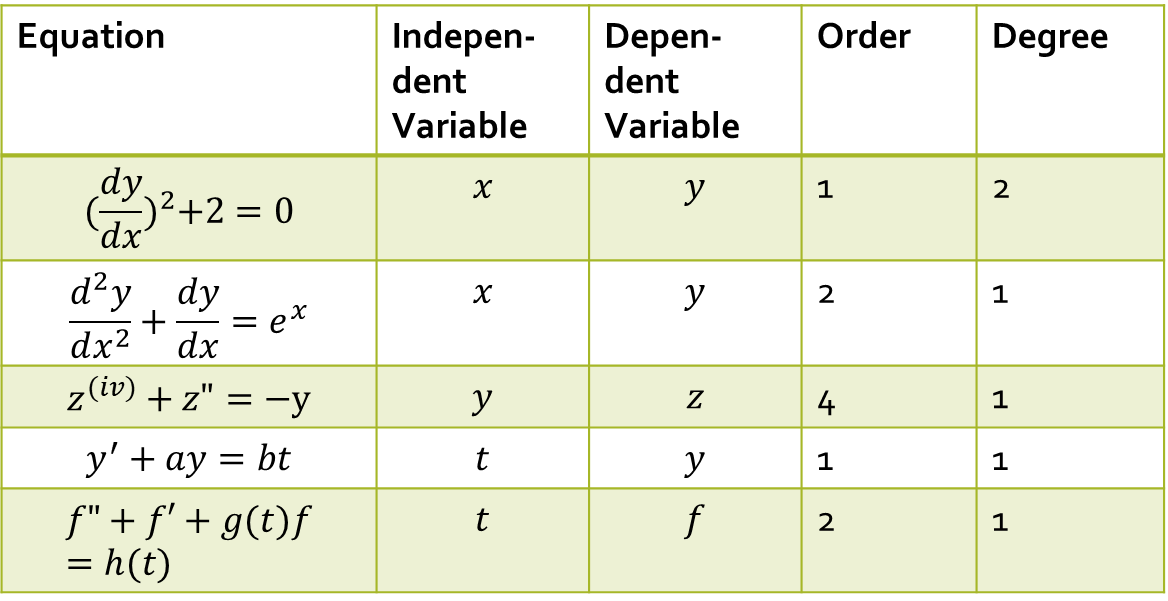
Definition, order, and degree, general and particular solutions of a differential equation
An equation with a derivative of one or more dependent variables, with one or more independent variables, is a differential equation (DE). Differential Equations are classified by type, order, and linearity of the equation. There are two main types of differential equations: “ordinary” and “partial”.
Differential equations with ONE independent variable are called ordinary differential equations.
Examples:
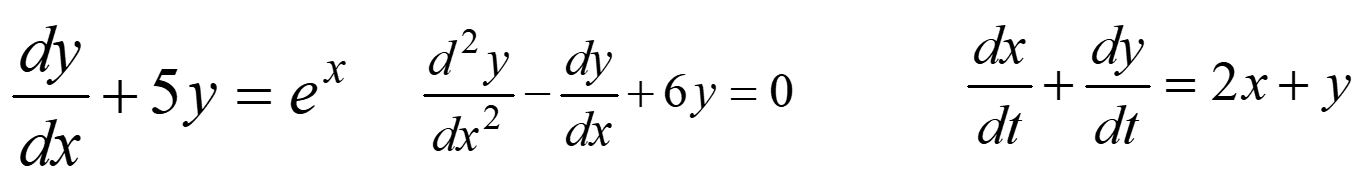
Differential equations with two or more independent variables are called partial differential equations.
Examples:
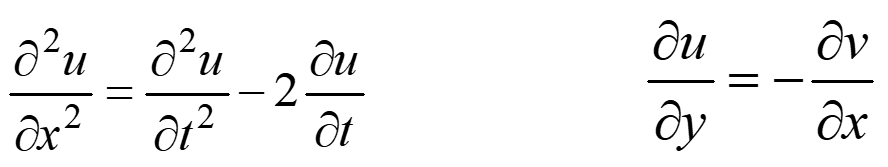
The order of a differential equation is the order of the highest derivative for a differential equation.
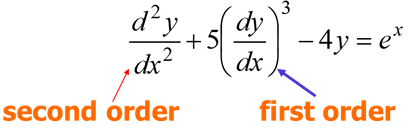
For instance, y’ = 4y is a first-order differential equation.
The second-order differential equation s”(t) = –32 has the general solution
s(t) = –16t2 + C1t +C2 General solution of s”(t) = –32
which contains two arbitrary constants.
Hence, the differential equation of order n has a general solution with n arbitrary constants.
A differential equation is called linear if there are no multiplications among dependent variables and their derivatives. In other words, all coefficients are functions of independent variables. Differential equations that do not satisfy the definition of linear are non-linear.
A solution to a differential equation is a function that satisfies the equation.
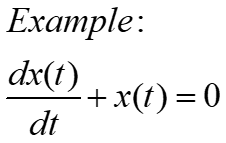
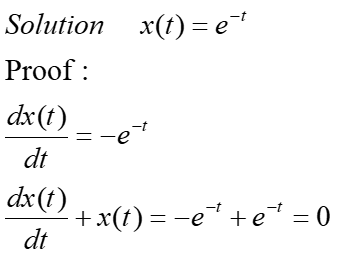
General Solution: Solutions obtained from integrating DE are called general solutions. The general solution of an order ordinary differential equation has arbitrary constants. For example, differentiation and substitution would show that y = e–2x is a solution of the differential equation
y’ + 2y = 0.
Likewise, every solution of this differential equation is of the form
y = Ce–2x General solution of y ‘ + 2y = 0
where C is any real number.
Particular Solution is the solutions found by putting specific values to the arbitrary constants in the general solutions. Particular solutions of a differential equation are deduced from initial conditions of the dependent variable or one of its derivatives for particular values of the independent variable
Singular Solutions: Solutions that can not be expressed by the general solutions are called singular solutions.
Analytical Solutions to ODE are available for linear ODE as well as several special classes of nonlinear differential equations. The numerical method is used to obtain a graph or a table of the unknown function
For instance, the second-order differential equation
s”(t) = –32having the general solution
s(t) = –16t2 + C1t +C2 General solution of s”(t) = –32
might have the following initial conditions.
s(0) = 80, s’(0) = 64 Initial conditions
Here, the initial conditions yield a particular solution
s(t) = –16t2 + 64t + 80. Particular solution
For the differential equation xy’– 3y = 0, verify that y =Cx3 is a solution. Then find the particular solution determined by the initial condition y = 2 when x = –3.
Solution:
Note that: y = Cx3 is a solution because y’ = 3Cx2 and
xy’– 3y = x(3Cx2) – 3(Cx3)
= 0.
Example: Classify the following DE:
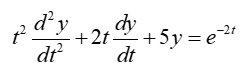
The DE is linear as no coefficients are functions of y and no higher degree terms in y or its derivatives.The DE is an ordinary type because y is a function of t only.
Solving a differential equation means finding an expression for y in terms of x or for A in terms of t without the derivative.