The solution of differential equations by the method of separation of variables solutions of homogeneous differential equations of the first order and first degree
Method of separation of variables is one of the most widely used techniques to solve ODE. It is based on the assumption that the solution of the equation is separable. This means that the final solution can be represented as a product of several functions.Each of these functions is only dependent upon a single independent variable.
Consider the first-order equation:
$\frac{dy}{dx}=f(x, y)$
If F (x, y) can be expressed as a function g (x) h(y), where, g(x) is a function of x while h(y) is a function of y, then we can assume that the differential equation of f(x, y) is said to be of variable separable type. The differential equation then has the form:
$\frac{dy}{dx}=h(y)\cdot g(x)$
Assume h ≠ 0, Then we can also write DE by separating the variables:
$\frac{1}{h(y)}dy=g(x)dx$
Now we can integrate both the sides of the equation to find the solution:
$\int{\frac{1}{h(y)}dy}=\int{g(x)dx}$
$H(y)=G(x)+C$
In this case, H(y) and G(x) are the antiderivatives of y and x respectively and C is the arbitrary constant.
Example: Solve the equation below giving the answer in the form y = f(x)
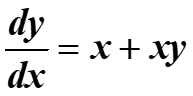
We first take out x as a common factor on the r.h.s., so
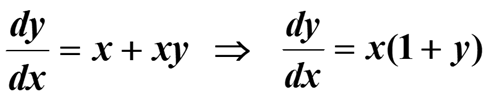
We can now separate the variables by dividing by (1 +y)
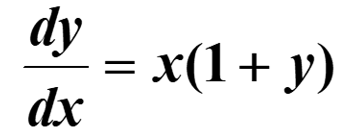
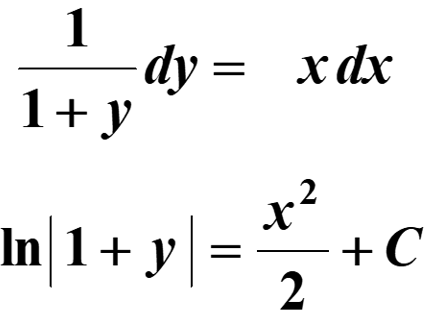
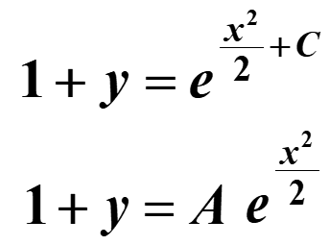
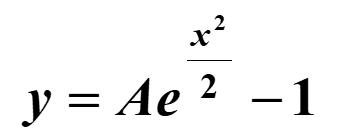
Example: Find the equation of a curve passing through the point (–1, 3), given that the slope of the tangent to the curve at any point (x, y) is $
\frac{2x}{y^{2 }}$
The equation for the slope of a tangent is: $\frac{dy}{dx}=\frac{2x}{y^{2 }}$
We now separate the x and y variables: $y^{2 }dy=2x dx$
This equation can be integrated on both sides:
$\int{y^{2 }dy}=\int{2x dx}$
$\frac{y^{3}}{3}=x^{2}+C$
Substituting x = –1, y = 3 in equation above, we get C = 8.
Substituting the value of C in the equation, we get the equation of the required curve as:
$\frac{y^{3}}{3}=x^{2}+8 $
Example: In a bank, the principal increases continuously at a rate of 5% per year. In how many years Rs 10000 double itself?
Solution: Let P be the principal at a certain time t. From the previous knowledge of simple interest, recall that:
$\frac{dp}{dt}=(\frac{5}{100})\times P$
$\frac{dp}{dt}=\frac{P}{20}$
Now we can separate the x and y variables on either side and integrate the equations:
$\int{\frac{dp}{P}}=\int{\frac{dt}{20}}$
$\log P=\frac{t}{20}+c$
$P= e^{\frac{t}{20}}\cdot e^{c}$
Let $e^{c}=C$, then we can write:
$P= Ce^{\frac{t}{20}}$
Substituting the values of P = 10000 at t = 0, we obtain C:
$10000= Ce^{0}, C=10000$
THerefpre, the solution is:
$P= 10000e^{\frac{t}{20}}$
To find the time to double the principle we substitute the value of P = 20000 in the equation above:
$20000= 10000e^{\frac{t}{20}}$
$2= e^{\frac{t}{20}}$
$t=20\log 2$