An elementary matrix is expressed by performing a single elementary row operation on an identity matrix.The operation on a row is denoted by the notation Ri and column operation is denoted using the notation Cj while k represents the scalar quantity. There are three types of elementary row operations:
1. Interchange two rows or columns of a matrix. Ri ↔ Rj and Ci ↔ Cj
For example, applying R1↔R2 to a matrix A = $\lbrack
\begin{matrix}
1 & 4 & \\
9 & 6 & \\
\end{matrix}
\rbrack $, we obtain $\lbrack \begin{matrix}
9 & 6 & \\
1 & 4 & \\
\end{matrix}
\rbrack $
2. Change a row by adding to it a multiple of another row, Ri → Ri + kRj and Ci → Ci + kCj .
For example, applying R2R2 – 2R1, to P = $
\lbrack \begin{matrix}
1 & 2 & \\
2 & -1 & \\
\end{matrix}
\rbrack $, we obtain $\lbrack \begin{matrix}
1 & 2 & \\
0 & -5 & \\
\end{matrix}
\rbrack $
3. Multiply each element in a row by the same nonzero scalar number, k. Ri → k Ri and Cj → kCj.
For example, by applying C3, to B = $
\lbrack \begin{matrix}
1 & 2 & 1 & \\
-1 & 3 & 1 & \\
\end{matrix}
\rbrack $, we obtain$\lbrack \begin{matrix}
1 & 2 & \frac{1}{2} & \\
-1 & 3 & \frac{1}{2} & \\
\end{matrix}
\rbrack $
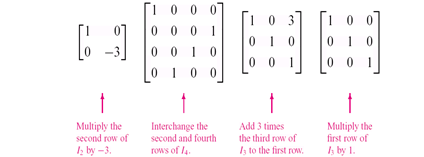
Likewise, the interchange of two equations, addition or multiplication does not alter the solution set. We can undo these steps by simple operations, for example, we can undo by multiplying the new equation by 1/c (since c ≠ 0), producing the original equation.
Example: Compute E1A, E2A, and E3A, and show how these products are obtained by elementary row operations on A.
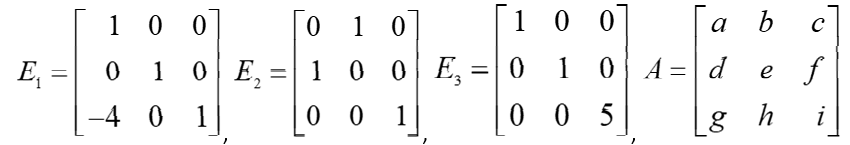
An interchange of R1 and R2 of A produces E2A and multiplication of R35R3 produces E3A. Left-multiplication by E1 in Example 1 has the same effect on any 3 X n matrix.Since E1∙ I = E1, we see that E1 itself is produced by this same row operation on the identity.
Therefore, If an elementary row operation is performed on an m x n matrix A, the resulting matrix can be written as EA. In this case, the m x m matrix E is created by putting the same row operation on Im.Each elementary matrix E is invertible. Note that, the inverse of E is the elementary matrix and it is of the same type that transforms E back into I.To calculate the inverse of matrix A, we apply the elementary row operations on the augmented matrix [A I] and reduce this matrix to the form of [I B]. The right-hand side of this augmented matrix B is the inverse of A.
Example: Consider the matrix:$A=\lbrack \begin{matrix}
1 & 0 & 2 & 3 & \\
2 & -1 & 3 & 6 & \\
1 & 4 & 4 & 0 & \\
\end{matrix}
\rbrack $ and $E=\lbrack \begin{matrix}
1 & 0 & 0 & \\
0 & 1 & 0 & \\
3 & 0 & 1 & \\
\end{matrix}
\rbrack $.
The elementary matrix provides EA$=\lbrack \begin{matrix}
1 & 0 & 2 & 3 & \\
2 & -1 & 3 & 6 & \\
4 & 4 & 10 & 9 & \\
\end{matrix}
\rbrack $.
This is the same matrix as A that results when we add 3 times the first row of A to the third row.