Validating the statements involving the connecting words difference between contradiction, converse and contrapositive
Rule 1: If p and q are mathematical statements, then to show that ‘p and q’ are true, follow the steps below:
- Show that p is a true statement
- Show that q is a true statement
For statements with ‘or’
Rule 2: If p and q are mathematical statements, then to show that p and q are true statements, follow the steps below:
- Assuming that p is a false statement, show that q must be true.
- Assuming that q is false, show that p must be true.
For statements with ‘if-then’
Rule 3: To prove the if p then q statements, we need to verify that any one of the following cases must be true
- Assuming that p is true, use the direct method to show that q is true
- Assuming that q is false, use the contrapositive method to show that p must be false
For statements with “if and only if”
Rule 4: To prove that the statement“ p if and only if q” is valid, we need to show that
- If p is true, then q is true and
- If q is true, then p is also true
- If p is false then q is also false and vice verse
A conditional statement has two parts to understand, these are a hypothesis and a conclusion.
When the if-then form is used to write a conditional statement, the part after the “if” is the hypothesis, and the part after the “then” is the conclusion. It is written as p → q
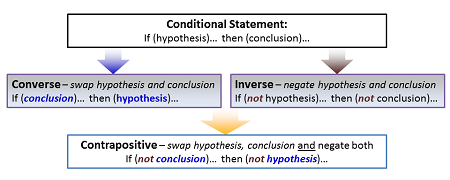
The converse of a conditional statement can be obtained by exchanging the hypothesis and the conclusion.The converse of p → q is written as q → p
The inverse is the statement that we obtain by negating the hypothesis and conclusion: ~p ~q
A contradiction, c is a statement form that is false regardless of the truth values of the statement variables. The statement for p Λ ~ p is a contradiction.
A contrapositive negates the hypothesis and the conclusion of the converse. The contrapositive of p → q is written as ~q → ~p.
When any two statements together are either both true or both false
- A conditional statement is equivalent to its contrapositive.
- The inverse and the converse of any conditional are equivalent.
Below are the truth values of the related statements above. Equivalent statements have the same truth value.

Example: If an animal is a cat, then it has four paws.
Converse: If an animal has 4 paws, then it is a lion.
There are other animals that have 4 paws that are not lions, so the converse is false.
Inverse: If an animal is not a lion, then it does not have 4 paws.
There are animals that are not the lion that have 4 paws, so the inverse is false.
Contrapositive: If an animal does not have 4 paws, then it is not a lion; True. Lions have 4 paws, so the contrapositive is true.