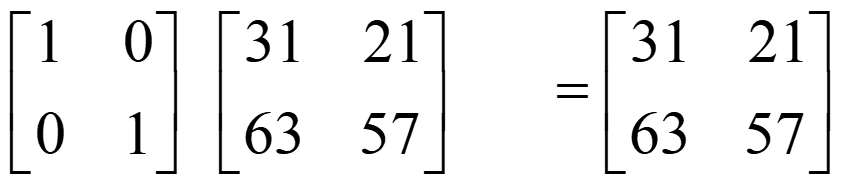Operation on matrices: Addition and multiplication and multiplication with a scalar
For adding and subtracting matrices, they must have the same order, mxn. To add matrices of the same order, add their corresponding elements and to subtract matrices of the same order, subtract their corresponding elements. The following mathematical notation can be used:
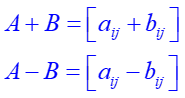
Note that the sum or subtraction of two matrices of the same size yields a matrix of the same size. Therefore, matrices of different sizes can not be added to subtract.
![]()
Example: Add the matrices:
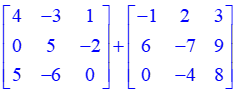
First, make sure that each matrix is 3X3, to perform the addition. Adding corresponding entries we have

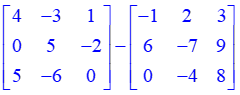
Example: Subtract the matrices:
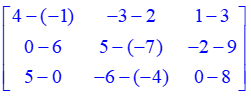
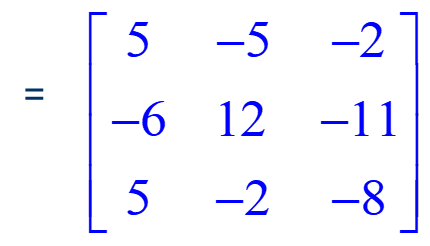
The product of two matrices is another matrix. The method of multiplication of matrices is not as intuitive but this method is important in many mathematical applications.Two matrices A and B need to be conformable to allow multiplication. This means that the number of columns of A is equal to the number of rows of B. If A is an m x p matrix and B is a p x n matrix, then their matrix product is denoted by AB, which is an m x n matrix. Their element in the ith row and jth column is the real number obtained from the product of the Ith row of A and the jth column of B. Note that when the number of columns of A does not equal the number of rows of B, the matrix product AB is not defined. For example, a row matrix consists of 2 rows of 5 numbers so this matrix has five columns. It has dimensions 2 X 5. This matrix can be multiplied by a column matrix consisting of 5 numbers in a single column (this matrix has dimensions 5X2).
Example: Multiplication of matrices
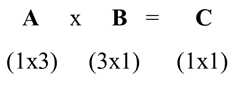
Successive multiplication of row i of A with column j of B can be explained as row by column multiplication
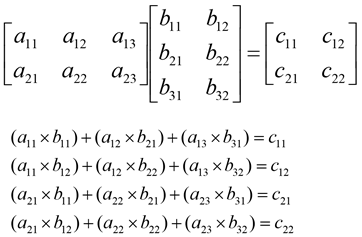
Matrices can be multiplied by a scalar element which is singular or constant.The scalar product of a number k and a matrix A is the matrix that can be denoted by kA. It is obtained by multiplying each entry of A by the number k. In mathematical notation, let k be a scalar quantity; then:
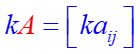
Example: If k=4 and
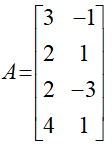
Properties:
- k (A + B) = kA + kB
- (k + g)A = kA + gA
- k(AB) = (kA)B = A(k)B
- k(gA) = (kg)A
Recall that, IA = A