Trigonometric functions are continuous at all points
Tangent and secant are flowing regularly everywhere in their domain, which is the combination of all exact numbers.
Let a be a real number in the domain of a given trigonometric function, then
- $\lim _{x\to a}\sin x=\sin a$
- $\lim _{x\to a}\cos x=\cos a$
- $\lim _{x\to a}\tan x=\tan a$
- $\lim _{x\to a}\cot x=\cot a$
- $\lim _{x\to a}\sec x=\sec a$
- $\lim _{x\to a}\csc x=\csc a$
Special cases:
- $\lim _{x\to 0}\frac{\sin x}{x}=1$
- $\lim _{x\to 0}\frac{1-cos x}{x}=0$
Hence you can obtain
$\lim _{x\to 0}\frac{\tan x}{x}=(\lim _{x\to 0}\frac{\sin x}{x})(\lim _{x\to 0}\frac{1}{\cos x})=(1)(1)=1$
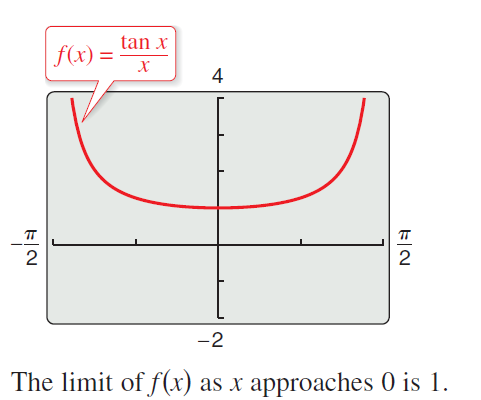
For example:
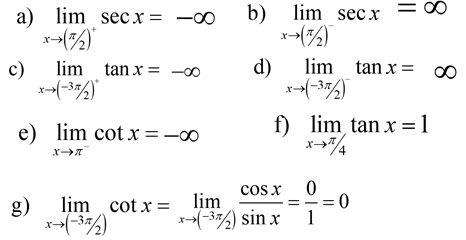
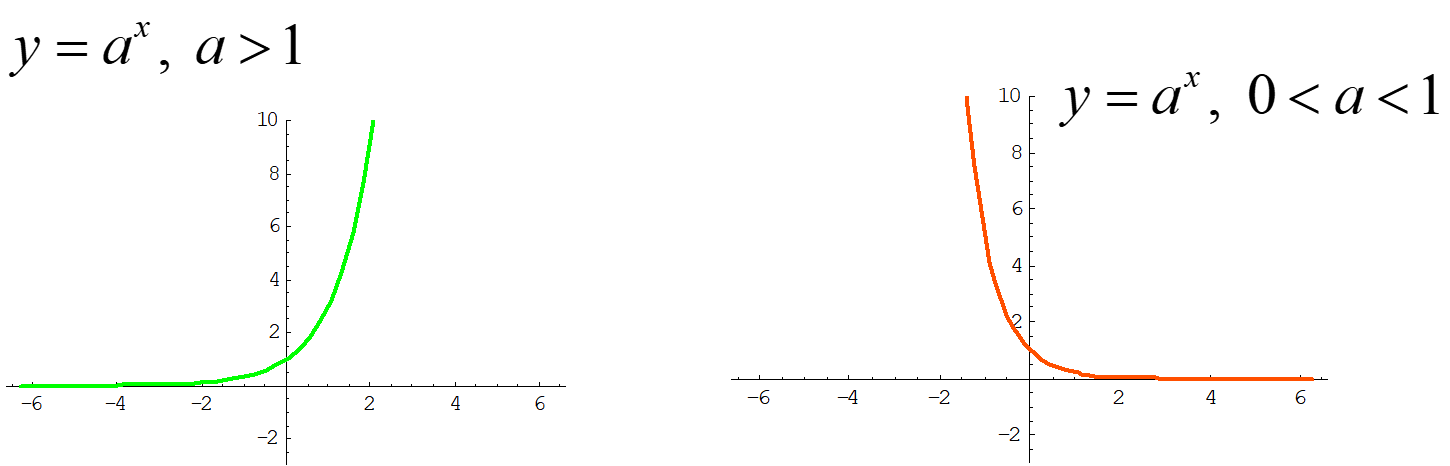
The exponential functions are continuous at every point.

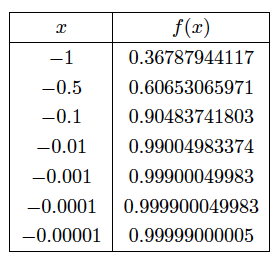
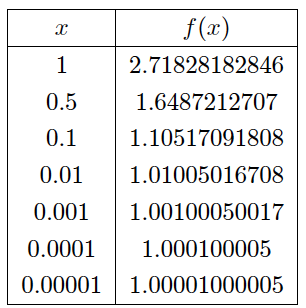
Example: Evaluate $\lim _{x\to 0}e^{x}$
We begin by constructing a table for the values of f(x) = e$^{x}$ and plotting the values close to but not equal to 0. Tables below show $\lim _{x\to 0^{-}}e^{x}=\lim _{x\to 0^{+}}e^{x}=1$
Limit laws for exponential function:
$\lim _{x\to \infty }e^{x}=\infty $;
$\lim _{x\to -\infty }e^{x}=0$;
$\lim _{x\to \infty }e^{-x}=0$;
$\lim _{x\to -\infty }e^{-x}=\infty $;
The motive of this set of laws was to show that if the exponent of an exponential goes to infinity in the limit then the exponential function will also go to infinity in the limit. Similar to it, if the exponent flows to minus infinity in the limit then the exponential will flow to 0 in the limit.
Example: Evaluate $\lim _{x\to \infty }e^{10x}-4e^{6x}+15e^{6x}+45e^{x}+2e^{-2x}-18e^{-48x}$
By taking the limit of each exponential terms we get:
$\lim _{x\to \infty }e^{10x}-4e^{6x}+15e^{6x}+45e^{x}+2e^{-2x}-18e^{-48x}=\infty -\infty +\infty +0-0=\infty $
The logarithm rule is valid for any real number b>0 where b≠1
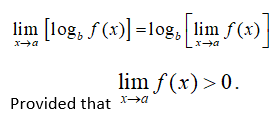
Example: Evaluate $\lim _{x\to 1}\ln x$
We begin by constructing a table for the values of f(x) = ln x and plotting the values close to but not equal to 1. Tables below show $\lim _{x\to 1^{-}}\ln x=\lim _{x\to 1^{+}}\ln x=0$
We begin by constructing a table for the values of f(x) = ln x and plotting the values close to but not equal to 1. Tables below show
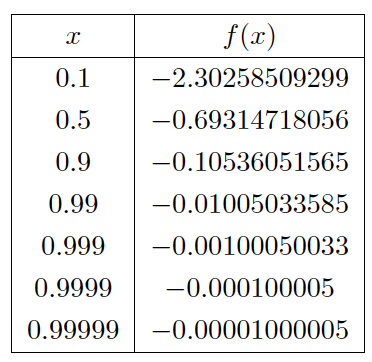
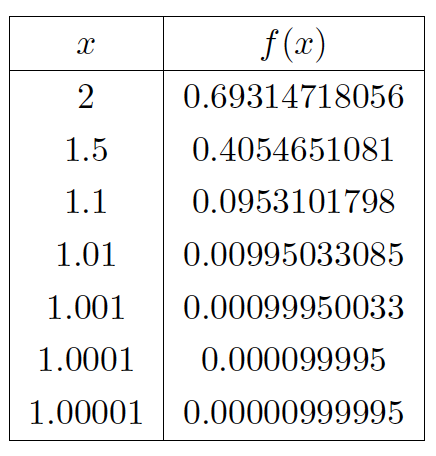
Limit laws for logarithmic function:
$\lim _{x\to 0^{+}}\ln x=-\infty $; $\lim _{x\to \infty }\ln x=\infty $
The right-handed limit was operated for $\lim _{x\to 0^{+}}\ln x=-\infty $ since we cannot put negative x’s into a logarithm function. This means that the normal limit cannot exist because x from the right and left side of the point in question should both be evaluated while x’s to the left of zero are negative. We can see that if the argument of a log goes to zero from the right (i.e. always positive) then the log goes to negative infinity in the limit while if the argument goes to infinity then the log also goes to infinity in the limit. Note as well that we can’t look at a limit of a logarithm as x approaches minus infinity since we can’t plug negative numbers into the logarithm.