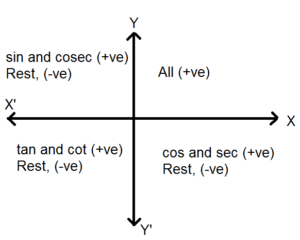
Trigonometric functions of sine, cosine, tangent, cotangent are based on the signs of y and x coordinates in the respective four quadrants.
| θ lies in which Quadrant | I | II | III | IV |
| Trigonometric functions | ||||
| Sin θ | +ve | +ve | -ve | -ve |
| Cos θ | +ve | -ve | -ve | +ve |
| Tan θ | +ve | -ve | +ve | -ve |
| Cot θ | +ve | -ve | +ve | -ve |
| Cosec θ | +ve | +ve | -ve | -ve |
| Sec θ | +ve | -ve | -ve | +ve |

From the above,
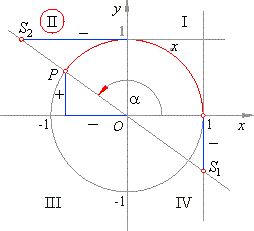
Quadrant I: The values of the trigonometric functions including Sine, Cosine, Tangent, Cotangent of any of the arc from the I Quadrant are the positive ones as coordinates are positive of the given points – P, S₁, and S₂, which define their specific values.
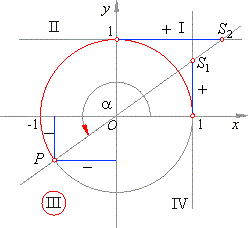
Quadrant II: From the 2nd quadrant points, for the arcs, P & S₂, both consist of negative abscissas (in the figure above), so, cotangent and the cosine exist as negative. Terminal point P’s ordinate is +ve so that Sine is +ve while ordinate of Point S₁ is -ve and hence, the tangent is negative.
( 
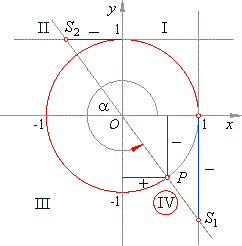
Quadrant III: As abscissas plus terminal points P’s ordinates of arcs from the 3rd quadrant (see the figure above) are -ve. It follows the sine and cosine functions of the given arcs are -ve. Point S1’s ordinates plus point S2’s abscissa which belongs to arc from the III quadrant are +ve. Therefore, cotangent and tangent of the given arcs are +ve.
Quadrant IV: The functions including tangent, sine, and cotangent of the given arcs from IVth quadrant are -ve, similar to points S₁, S₂, and P’s coordinates which do belongs to them only. Only arc’s cosine functions from IVth quadrant is +ve are point P’s abscissas which belongs to them as you can see in the figure above.
| Quadrant | Values of arc | Sin x | Cos x | Tan x | Cot x |
| I | From 0 to 90º | + | + | + | + |
| II | From 90º to 180º | + | – | – | – |
| III | From 180º to 270º | – | – | + | + |
| IV | From 270º to 360º | – | + | – | – |
Example
Question 1: Give signs of the trigonometric functions
Solution: Sine 146º = Sin (90º + 56º) = As Sine lies from 0º to 90º, therefore, The sign will be positive.
Question 2: Cos 455º
Solution: Cos (360º + 95º) = Cos (90º + 5º) = Cos 5º
From the above solution, it clearly means that the sign is positive.
Question 3: Tan 573º
Solution: Tan (360º + 213º) = Tan (180º + 33º) = Tan 33º
Hence, Tan 573º is positive