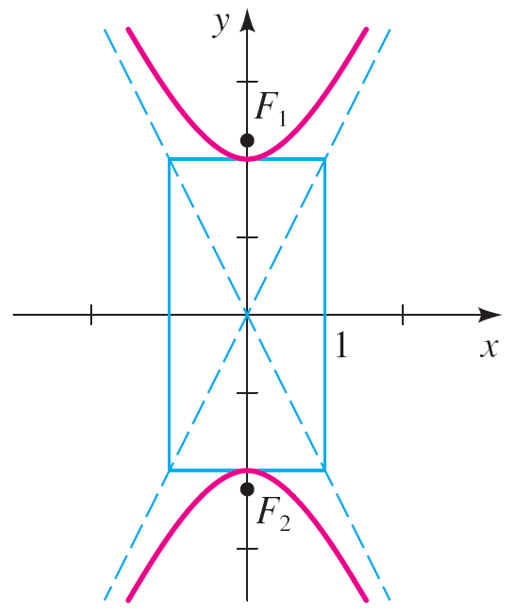
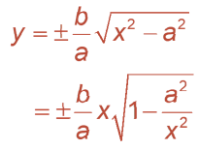Conic sections: Standard equation and simple properties of Hyperbola
The standard form of the equation of a hyperbola is developed in a similar methodology to an ellipse. Note, however, that a, b and c are related differently for hyperbolas than for ellipses.For a hyperbola, the distance between the foci and the centre is greater than the distance between the vertices and the centre.

This equation is the standard form of the equation of a hyperbola centred at the origin with the x-axis as its focal axis. When the y-axis is the focal axis:
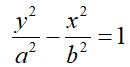
The values a, b, and c, are associated by the distance formula c2 = a2 + b2. Also, note that the length of the transverse axis = 2a and the length of the conjugate = 2b.
Standard Form for the Equation of a Hyperbola (Center at (0,0))

As with circles and ellipses, hyperbolas do not have to be centred at the origin.
Standard Form for the Equation of a Hyperbola (Center at (h,k))

Asymptotes are an essential aid for graphing a hyperbola. They help us determine its shape. The asymptotes mentioned are lines that the hyperbola approaches for large values of x and y.To find the asymptotes in the first case, we solve the equation for y to get:
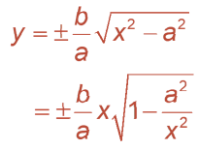
As x enlarges, a2/x2 goes closer to zero, therefore, as x → ∞, a2/x2 → 0. So, for large x,the value of y = ±(b/a)x. This shows that these lines are asymptotes of the hyperbola. The conjugate axis of a hyperbola is the line segment of length 2b joining (h, k + b) and (h, k – b) when the transverse axis is horizontal. When the transverse axis is vertical, the conjugate axis is the line segment of length 2b joining (h + b, k) and (h – b, k).
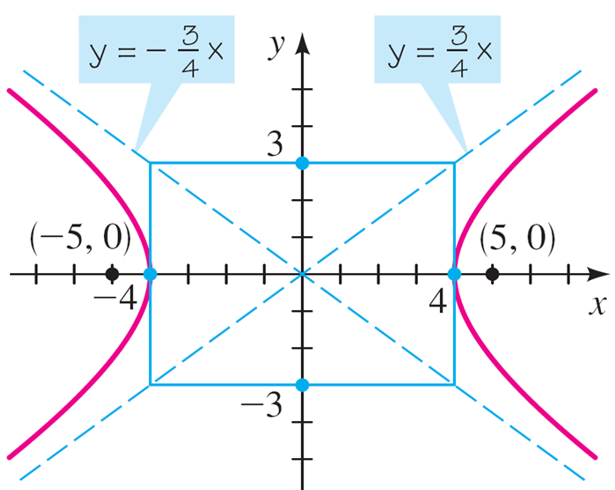
Example 1. A hyperbola has the equation 9x2 – 16y2 = 144. Find the vertices, foci, and asymptotes,
and sketch the graph.
First, we divide both sides of the equation by 144 to put it into the standard form:
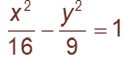
Since the x2-term is +ive, horizontal transverse axis occurs.Its vertices and foci are on the x-axis. Since a2 = 16 and b2 = 9, we get a = 4, b = 3, and $c=\sqrt{16+9}=5$.Thus, Vertices:(±4, 0), Foci: (±5, 0) and Asymptotes: y = ±¾x.
Example 2. Find the equation and the foci of the hyperbola with vertices (0, ±2) and asymptotes y = ±2x.
The hyperbola has a vertical transverse axis with a = 2 as the vertices are placed on the y-axis. From the asymptote equation, we see a/b = 2. We find a = 2, so 2/b = 2; thus, b = 1.
The equation is:
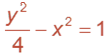
To find the foci,
c2 = a2 + b2= 22 + 12 = 5 .So, c = $\sqrt{5}$
Thus, the foci are (0, ± $\sqrt{5}$).