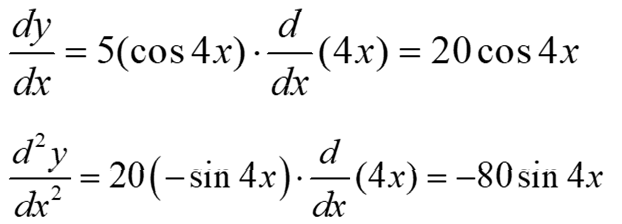Logarithmic differentiation, derivative of functions expressed in parametric forms. Second-order derivatives
The understanding of derivatives involving complicated functions involving products, quotients, or powers can often be simplified by using logarithmic functions. The method used in the following example is called logarithmic differentiation.
Example: Differentiate:
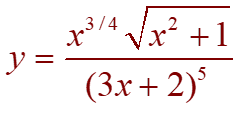
We take logarithms on both sides of the equation and then use the Log Laws to simplify:
![]()
Differentiating implicitly with respect to x gives:
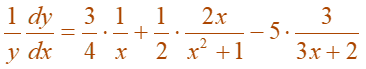
Solving for dy/ dx, we get:
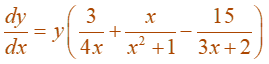
Here, we obtain an explicit expression for y, we can substitute and write:
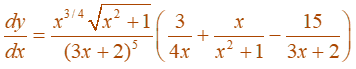
In general, four cases of exponents and bases are as follows:
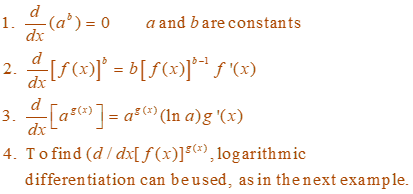
Some relationships involving 2 or more variables are complicated enough that we sometimes introduce a third quantity or variable in order to make things easier to handle. , The third quantity is mathematically named as a parameter. Instead of one equation relating say, x and y, we have two equations, one relating x with the parameter, and one relating y with the parameter.
For example, if (x, y) is a point in the graph where (x, y) depends on t, then both x and y are a function of t.
Let x = t2 and y = 2t at time t = 3, then
X = 32 = 9 and y = 2(3) = 6. Hence the coordinates of the point at t =3 are (9, 6)
An equation for x and y in terms of t is known as a parametric equation, with t being the parameter
Example: A curve is defined by the parametric equations given below:
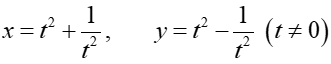
Find an expression for dy/dx in terms of t, and simplify your answer:
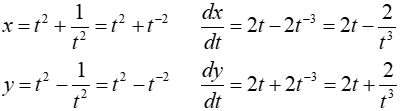
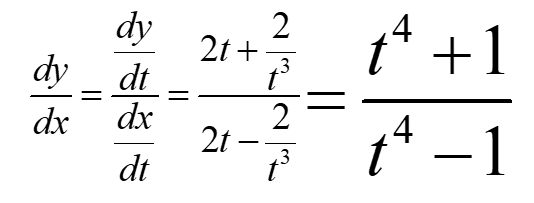
From this example, we can also conclude with respect to t that,
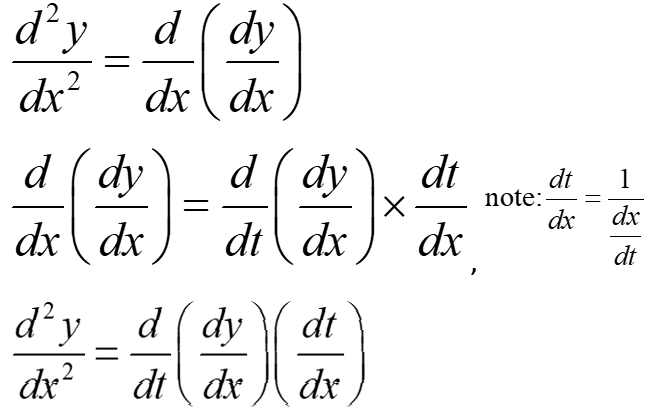
Consider an example from mechanics, We can obtain a velocity function by differentiating a position function. Likewise, we an acceleration function by differentiating a velocity function. Alternatively, we can assume that an acceleration function can be obtained by differentiating a position function twice.
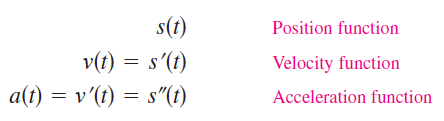
The function a(t) is the second derivative of s(t) and is denoted by s”(t). The second derivative is an example of a higher-order derivative as explained in the figure below.We can define derivatives of any positive integer order in the following manner. For instance, the third derivative is the derivative of the second derivative.
Higher-order derivatives are denoted as follows.
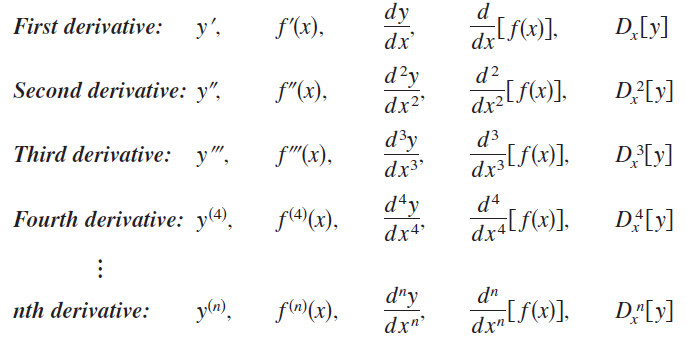
Example:Determine the 2nd derivative with respect to x of the function y = 5 sin 4x.