The binomial theorem or the binomial expansion is loaded with its extremely large applications and is immensely beneficial in the simplification of the lengthy calculations.
The binomial theorem or the expansion for the nth polynomial degree is given by:
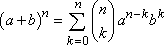
If there’s a need for the computation of (1+x)¹² which doesn’t mean that you to multiply the term 12 times but instead taking the help of the binomial expansion, it can be calculated within a few seconds.
For the discussion of the prime applications of the Binomial Expansion, they are as follows:
1.Problems based on Divisibility:
Assuming (1 + x)ⁿ = 1 + ⁿC₁x + ⁿC₂x² +…+ ⁿCₙxⁿ.
Taking any problem based on the divisibility, you have to first identify the values of x & n.
The given by which division has to be applied can be – x, x² or x³, however, the number present at the base is expressed in (1 + x) form, always.
This is, in fact, the easiest and most widely used binomial expression form.
2. Binomial Expression with Non- Positive Exponent
The features discussed previously were restricted to n, which is a positive integer. If “n” takes up any different value, then the binomial theorem is expressed as:
Let’s say, if it’s needed to figure out the value – (x+a)n n ∉ I⁺
If a>1, then it’s written in the form – aⁿ. (a + (x/a))ⁿ. This is given in the expanded form as:
aⁿ . (1+(x/n))ⁿ = aⁿ [1+n(x/a) + (n(n-1)/²) (x/a) + (n(n-1)(n-2))/3! (x/a)³ + ……∞]
Because “n” does not belong to the value of a positive integer, thus, the series on the right side will assemble for |x/a| < 1 only. Also, there exist finite terms in the binomial expansion opposite to the expansion for the “n” positive integer.
To note:
- It’s crucial to observe that in this condition, it’s not at all possible using ⁿCr symbol for the general term denotation.
- The binomial expansions in terms of ascending powers of “x” are only valid if the value of x is “small”. In the condition, when the value of x is large, that is, |x| > 1, then it’s much easier to expand this in 1/x powers.
- The below-mentioned expansions should be thought of as they give a helping hand to solve questions efficiently (for |x| <1).
(1 + x)⁻¹ = 1 – x + x^2 – x^3 + x^5 – ….. ∞
(1 – x)⁻¹ = 1 + x + x^2 + x^3 + x^4 + ….. ∞
(1 + x)⁻² = 1 – 2x + 3x^2 – 4x^3 + ….. ∞
(1 – x)⁻² = 1 + 2x + 3x^2 + 4x^3 + ….. ∞
3. Multinomial Expression:
Binomial Expansion’s generalized form is known as the Multinomial Expansion. When there exist more than 2 terms, then this case is thought-out to be the multinomial expansion.
If n ∈ N, the multinomial expansion’s next general term will be (x1 + x2 + x3 +…+ xk)ⁿ is (n!/a1!a2!…ak!) (x₁^a¹,x₂^a²,..…xₖ^a.k ), where a₁ + a₂ + a₃ + …………aₖ = n & a < ai < n, i = 1, 2, 3, …… k & the expansion having total no. of terms in the form ⁿ⁺ᵏ⁻¹Cₙ₋₁.
4. Rational Index
Another Binomial application is regarding rational index. This occurs when you alter the binomial from one form to another form like this:
- (1 + x)n, is the value where x’s absolute value is less than one & n can either be a fraction or an integer.
You can pretty easily get this form on the division of your binomial by “a” in the form:
- (a + b)5 => (1 + b / a)5
In the case (b / a), x’s absolute value is less than one for this particular expansion formula to operate.
Here’s the formula for using the rational index:
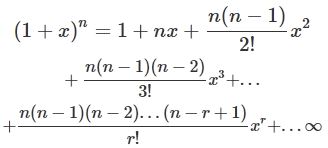
To use this Binomial Theorem form, it’s important to keep in mind that x’s absolute value is less than one. This formula can its applications in the field of integer, power, and fractions.
- As mentioned earlier, Binomial Theorem is widely used in probability area.
- It’s helpful in the economic sector to determine the chances of profit and loss.
- The binomial distribution and theorem are highly used for the calculation purpose.
- Binomial Theorem has a huge role to play in the future weather forecasting; as without binomial theorem, forecasting is just impossible.
- Forecasting of disaster is even dependent on the applications of binomial theorems.
- To give rankings to the candidates, binomial theorem plays a significant role.
- There’s extensive use of binomial in the architecture field to give shape and to determine the infrastructure areas for finding out what material’s amount has to be in use. It helps in calculating and finding out the total expenditure spent on the construction of the building. So, you can say that all the financial sites are indirectly dependent on the binomial theorem.