The mathematical function is a powerful tool used for business purposes, applications, the sciences, and engineering as they act in a manner of real-world aspect. To clearly understand the concept of functions and relations, you need to plunge a bit into ordered pairs, relations, and sets.
A function is illustrated as a special kind of relation from one kind to set to another one.
Considering the real world, the problems are specified systematically and are solved with the use of functions.
The understanding of relations is necessary so as to understand the given functions. And it’s required to understand the concept of Cartesian Products so as to understand the relations. A Cartesian Product belonging to two of the sets A and B refers to collection of whole of the ordered pairs (a,b) like a∈A and b∈B
A relation refers to Cartesian Product’s subset. Thus, the relation refers to a rule which relates the element from 1 set to the element from different or another set. Indeed, Function refers to a special relation’s kind.
Now, let’s look at the relation F, right from set A to set B.
Definition 1: Relation
F is assumed to be a function if each of its elements within set A is linked with exactly 1 element within set B.
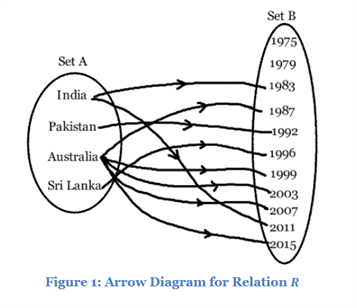
To have a better understanding in between the difference of the functions and relations, now, let us take any eg. Set A is having the countries’ names which have won the world cup of cricket and Set B includes those years in which that particular world cup was played.
The diagram in figure1 depicts the relation R but certainly it doesn’t represent a function. This is due to the elements in set A are correlated with more than 1 element considering set B.
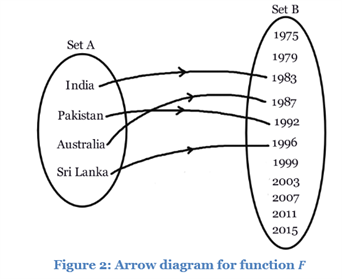
But, if you’re defining a relation F from the set A to the set B in the manner that it correlates with the countries accompanying that year in which they had for the first time won the cricket world cup and for each of the elements in Set A, we’ll have exactly 1 correlation in set B. This relation F which is represented in figure 2 certifies to be a function.
How to determine the function’s domain?
- To figure out the domain, it is required to see the values of independent variables that are acknowledged for the usage as described below that is no value of zero at fractions’ bottom and no sign of negative in the square brackets.
Range
- The set of entire outputs of the function is called function’s range i.e. x or After the substitution of the domain, the whole of the set of all the values which are possible as the conclusion of dependent variable which is y.
Let’s say, function’s range “F” is {years – 1983, 1992, 1987, 1996}. Differently, the whole set B is called function’s co-domain. It refers to the set that encompasses the entire function’s outputs.
Therefore, real numbers’ set refers to a codomain for each of the functions which are real-valued. Function’s codomain F is set B.
To determine Function’s range, How?
- The extension of the whole of the ‘y’ values, right from minimum value to maximum value – it’s the function’s range.
- As given in y’s expression, on substituting all x values for checking whether it’s +ve, -ve, or equal to the other values.
- Calculate maximum and minimum y values
- Accordingly, sketch the graph for same.
So as per conclusion,
- The range is calculated after we substitute the possible values of x for finding out the y values.
- Domain id explained as value’s entire set which is possible for the independent variables.