Probability: Connections with the theories of earlier classes
Nothing in life is certain and in all our activities, we gauge the chances of successful outcomes, from business to medicine to the weather. A probability helps in understanding a quantitative description of likelihoods associated with various outcomes. It helps in developing a bridge between descriptive and inferential statistics.
Probability is the chance that some event will happen and it is the ratio of the number of ways a certain even can occur to the total number of possible outcomes.
The probability ranges between 0 and 1. If an outcome cannot occur, then the probability of that event is 0. If there is a 100% certainty that an event shall occur then it has a probability of 1. The sum of probabilities of mutually exclusive outcomes is equal to 1.
P(M) + P(F) = 1
Calculate the probability of each independent event.
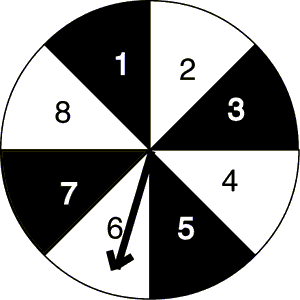
1) P(black) = 4/8
2) P(1) = 1/8
3) P(odd) = 1/2
4) P(prime) = 1/2
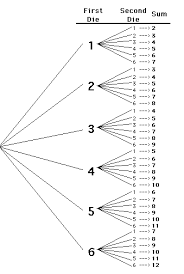
You can use a tree diagram to determine the sample space of rolling two dice. Six outcomes are possible for the first die {1,2,3,4,5,6}. These outcomes are represented by six branches of the tree starting from the “tree trunk” as shown in the figure below. For every six outcomes, there are six outcomes in the second die represented by the second branches. By using the fundamental counting principle, we can conclude that 6*6=36 outcomes.
As explained in the example above an experiment is said to have equally likely outcomes when each simple event has the same probability of occurring.If an experiment has n equally likely simple events or compound events that are mutually exclusive. If the number of outcomes for an event E to occur is m, then the probability of E, P(E), is
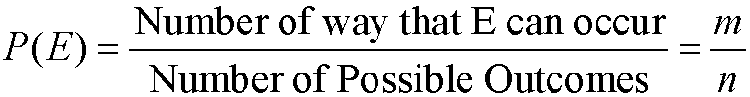
Likewise, if S is the sample space of a certain experiment with total n outcomes, then the possibility of E to occur is
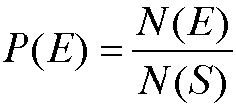
Venn diagrams are used to explain the events as circles enclosed in a rectangle. The rectangle shown below represents the sample space and each circle represents an event.
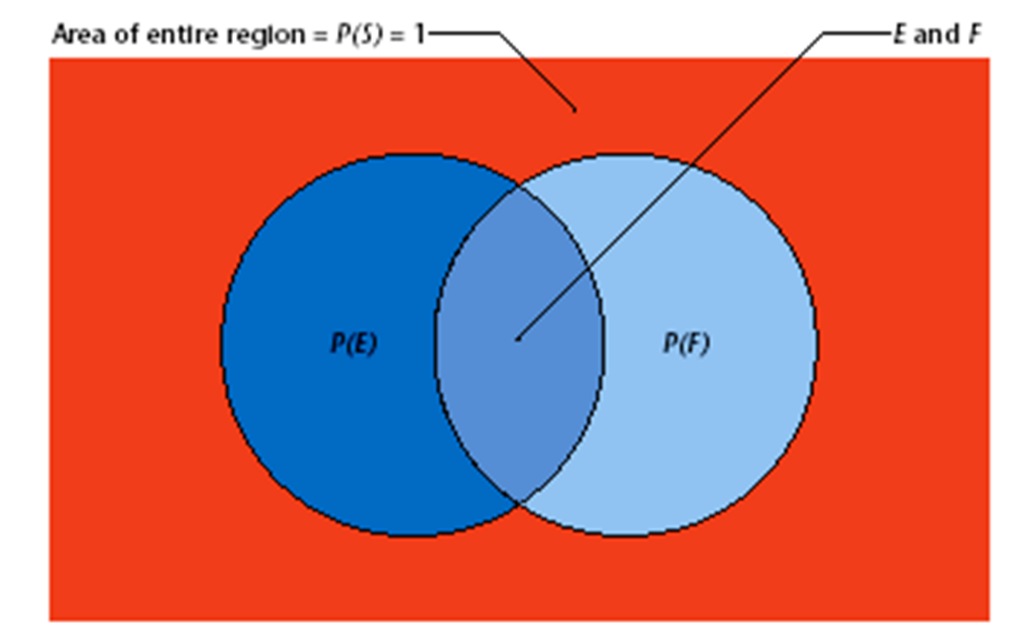
If events P and Q have no simple events in common or cannot occur simultaneously, they are said to be disjoint or mutually exclusive.Two events P and Q are independent if the occurrence of event P in a probability experiment does not affect the probability of event Q. Two events are dependent if the occurrence of event P in a probability experiment affects the probability of event Q.Two events P and Q are independent if:
P(Q| P) = P(Q) or P(P | Q) = P(P)