Exponential functions can be differentiated using the chain rule. One of the most intriguing and functional characteristics of the natural exponential function is that it is its own derivative.
In other words, it has solution to the differential equation being the same such that,y’ = y.The exponential function which has the property that the slope of the tangent line at (0,1) has the value m0 = 1 is called the natural exponential function. It can be written as exp(x) or more frequently as ex, where e is the base of the exponential function which has a unit slope at (0,1).
Let u be a differentiable function of x, then we can accept the following properties:
- $\frac{d}{dx}\lbrack e^{x}\rbrack =e^{x}$
- $\frac{d}{dx}\lbrack e^{u}\rbrack =e^{u}\cdot \frac{du}{dx}$
- $\frac{d}{dx}\lbrack e^{f(x)}\rbrack =e^{f(x)}\cdot f'(x)$
This can be proved using the limit formula:
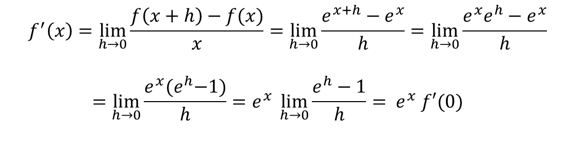

| h | $\frac{e^{h}-1}{h}$ |
| 1 | 1.71828 |
| 0.1 | 1.05171 |
| 0.01 | 1.00502 |
| 0.001 | 1.00050 |
| 0.0001 | 1.00005 |
| 0.00001 | 1.00001 |
$\frac{d}{dx}e^{x}=e^{x}$
We can use the chain rule to find the derivative of the a$^{x}$.
$y=a^{x}
\ln y=\ln a^{x}=x\ln a
a^{x}= e^{x\ln a}$
$\frac{d}{dx}a^{x}= \frac{d}{dx} (e^{x\ln a})= e^{x\ln a} \frac{d}{dx} (x\ln a)=e^{x\ln a} \cdot \ln a$
$\frac{d}{dx}a^{x}=a^{x}\cdot \ln a$
Example: Find the derivative of $f(x)=e^{3+5x}$
$f'(x)=e^{3+5x}\cdot \frac{d}{dx}(3+5x)$
$f'(x)=5e^{3+5x}$
Example: Differentiate the following function: y = e$^{tan x}$
Solution: Use chain rule, let u = tan x
Then, we have y = e$^{u}$.
Therefore, $\frac{dy}{dx}=\frac{dy}{dx}\cdot \frac{du}{dx} = e^{u}\frac{du}{dx}=e^{\tan x}\sec ^{2}x $
A derivative of natural logarithm function:
Let $y=\ln x$ such that x ≠ 0
Then,
$e^{y}=x$
$\frac{d}{dx}e^{y}= \frac{d}{dx} x$
$e^{y}\frac{dy}{dx}= 1$
$x\frac{dy}{dx}= 1$
$\frac{dy}{dx}=\frac{1}{x}$
$\frac{d}{dx}(\ln x)=\frac{1}{x}$
$\frac{d}{dx}(\ln f(x)=\frac{f'(x)}{f(x)};[f(x)>0]$
Example: Differentiatey = ln(x3 + 1).
Solution, Use chain rule to solve this function:
Let u = x3+1, then y = ln u
$\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}=\frac{1}{u}\cdot \frac{du}{dx}=\frac{1}{x^{3}+1}(3x^{2})=\frac{3x^{2}}{x^{3}+1}$
Example: Find $\frac{d}{dx}(\log _{a}x)$
Let y = logax. Then, ay = x.
We can differentiate the equation above implicitly with respect to x, we obtain: $a^{y}(lna)\frac{dy}{dx}=1$
Therefore, we obtain: $\frac{dy}{dx}=\frac{1}{a^{y}\ln a}=\frac{1}{x\ln a}$
If we put a = e in the above formula, then the factor on the right side becomes ln e =1and we get the formula for the derivative of the natural logarithmic function loge x =ln x.
$\frac{d}{dx}(\ln x)=\frac{1}{x}$
The differentiation formula can be manipulated in the simplest form when a = e because ofln e =1.
Example: Find f ’(x) if f(x) = ln |x|.
Solution: We know:
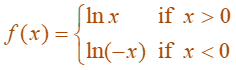
It follows that
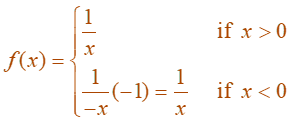
Thus, f’(x) = 1/x for all x not equal to 0.
Likewise, $\frac{d}{dx}\ln \vert x\vert =\frac{1}{x}$
Example: Differentiate $f(x)= \sqrt{\ln x}$
$f^{‘}(x)=\frac{1}{2}(\ln x)^{-\frac{1}{2}}\cdot \frac{d}{dx}(\ln x)=\frac{1}{2\sqrt{\ln x}}\cdot \frac{1}{x}=\frac{1}{2x\sqrt{\ln x}}$
Example: Differentiate y = ln(sin x)
$\frac{d}{dx}\ln (sinx)=\frac{1}{\sin x}\frac{d}{du}(\sin x)=\frac{1}{\sin x}\cos x=\cot x$