Probability: Occurrence of events: not, and, or events
The event, E, is any subset of the sample space, S that is a set of outcomes which does not necessarily need to have all outcomes for random phenomena. The event, E, is said to have occurred if after the outcome is observed then the outcome lies in E. Simple events are used to combine events in order to make other events and explain them using logical operations: and, or and not.
Example: Consider the probability experiment of having two children.
(a) Identify the simple events of the probability experiment of having two children.
Answer: (boy, girl ), (girl, girl ), ( boy, boy)
(b) Determine the sample space.
Answer: S = { (boy, girl), (girl, girl), (boy, boy)
(c) Define the event E = “have one boy” for the experiment.
E = (boy, girl), (boy, boy)
The probability of an event is denoted as P(E), and it is the likelihood of that event occurring.
The Null Event is an empty event that never occurs, φ = { } = the event that contains no outcome.
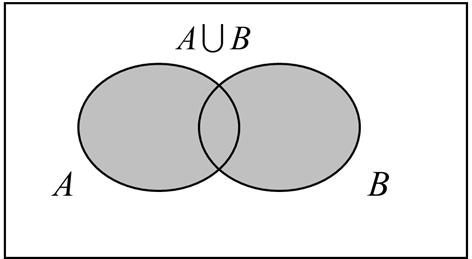
Let A and B be two events in a set, then the union of A and B is the event (denoted by A U B) defined by:
A U B = {e| e belongs to A or e belongs to B}
The event A U B occurs if event A occurs or the event and B occurs.
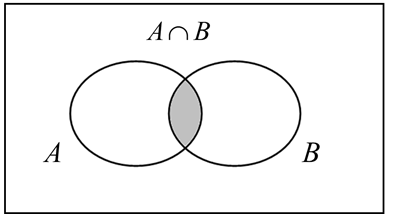
Let A and B be two events, then the intersection of A and B is the event (denoted by A∩B ) defined by:
A∩B = {e| e belongs to A and e belongs to B}
The event A∩B occurs if event A occurs and the event and B occurs.
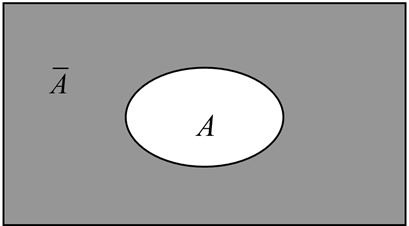
Let A be an event, then the complement of A (denoted by) defined by:
= {e| e does not belongs to A}
The event occurs if the event A does not occur
Note that, you are working with the union if you see the word or, intersection if you see the word and complement if you see the word not.
Two events A and B are called mutually exclusive if A ∩B = φ
If two events A and B are mutually exclusive, then they have no outcomes in common.
They can’t occur at the same time. The outcome of a random experiment cannot belong to both A and B subsets.