Definite integrals as a limit of a sum, Fundamental Theorem of Calculus (without proof)
If f(x) is a function defined for a ≤ x ≤ b, we divide the interval [a,b] into n subintervals of equal
width Δx = (b-a)/n. We assume x0 =a, x1, x2,…, xn (=b) which denote the endpoints of these subintervals and we let x1 *, x2 *,…, xn* be any sample points in these subintervals. Then, the definite integral of f from a to b is written in calculus as:
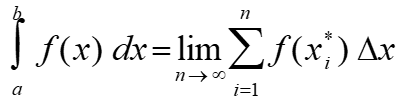
provided this limit exists and it should provide the same value for all possible choices of sample points. If the limit exists, we say f is integrable on [a,b]. In this case, a is the lower limit of integration, and the number bis the upper limit of integration.
The precise meaning of the limit that defines the integral can be explained as follows:
For every number ε> 0 N is an integer which follows and for every integer n>N and for every choice of xi* in [xi-1, xi] as shown below 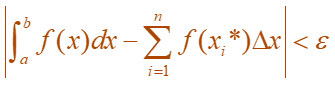
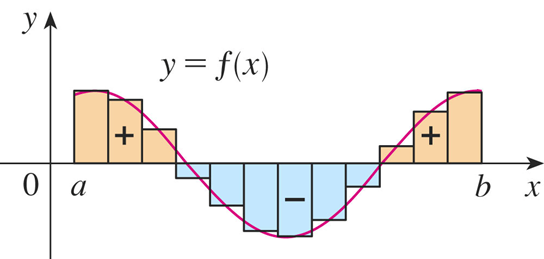
If f is continuous and nonnegative on the closed interval [a, b], then the area of the region bounded by the graph of f, the x-axis, and the vertical lines x = a and x = b can be interpreted as:
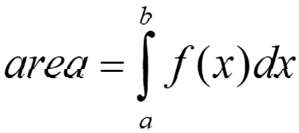
If the graph is nonpositive from a to b then
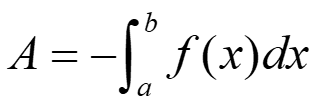
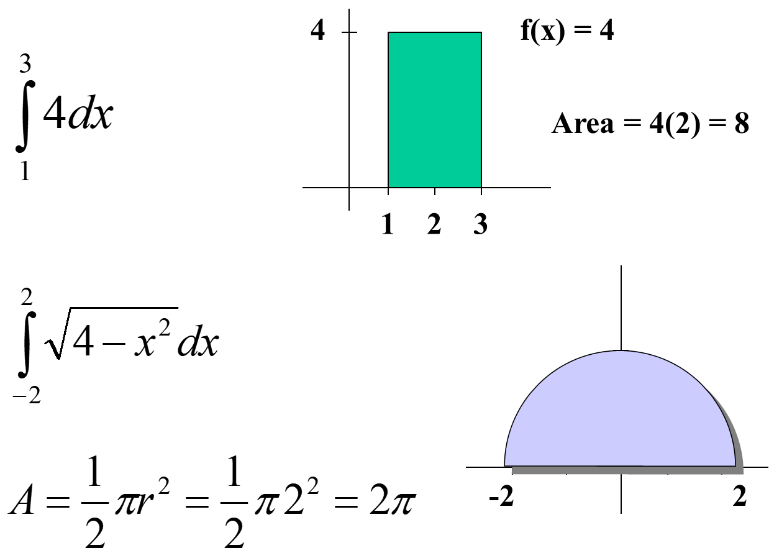
Areas of common geometric figures:
If f is continuous on [a, b], or if f has only a finite number of jump discontinuities, then
f is integrable on [a, b].That is, the definite integral $\int_{a}^{b}{f(x)dx}$ exists.
Let f be a continuous function defined on the closed interval [a, b] and F bean antiderivative of f. Then,
$\int_{a}^{b}{f(x)dx}=[F(x)]_{a}^{b}=F(b)-F(a)$
Definition of Two Special Definite Integrals:
- If f is defined at a fixed point x = a, then
- If f is integrable on [a, b], then
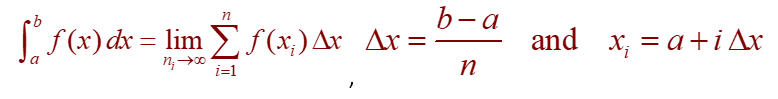
Example:
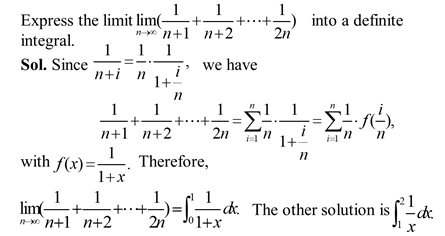
For calculating $\int_{a}^{b}{f(x)dx}$, use the following steps:
Find the indefinite integral∫ f x dx ( ) . Let this be F(x). There is no need to keep integration constant C because if we consider F(x) + C instead of F(x), we get $\int_{a}^{b}{f(x)dx}=[F(x)]_{a}^{b}=F(b)-F(a)$
Thus, the arbitrary constant disappears in evaluating the value of the definite integral and then we can evaluate the value of integral by plugging in b and a.
Example: Evaluate $\int_{0}^{1}{\frac{\tan ^{-1}x}{1+x^{2}}}$
Use substitution method, let t = $\tan ^{-1}x$ then dt = $dt= \frac{1}{1+x^{2}}dx$. In this case, the new limits for t are $x=0\to t=0;x=1\to t=\frac{\pi }{4}$
$\int_{0}^{1}{\frac{\tan ^{-1}x}{1+x^{2}}}=\int_{0}^{\frac{\pi }{4}}{t dt[\frac{t^{2}}{2}]_{0}^{\frac{\pi }{4}}}$
$\frac{1}{2}\lbrack \frac{\pi ^{2}}{16}-0\rbrack =\frac{\pi ^{2}}{32}$