Arithmetic Mean
The A.M or the Arithmetic Mean is referred to as the average of 2 given numbers. And if one A.M “A” is included between the two numbers which are “a” & “b”, then A is called the arithmetic mean present in between the numbers, a & b.
A.M. = A = $\frac{a+b}{2}$
Here, the number A is called the Arithmetic mean of a & b numbers. And as per the property of A.M., you can state that A – a = b – A i.e. it’s called the value‘d’, which is the common difference of the AP given.
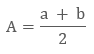
A.M is usually calculated for finding out sequence’s missing number between the 2 numbers given.
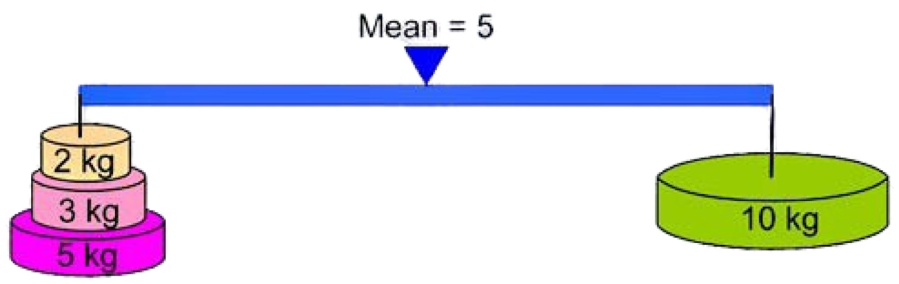
The AM acts as the point of balance for the 2 given numbers.
Example
What is A.M of 8 and 64?
Given
a = 8
b = 64
Therefore, the A.M is equal to
AM = $\frac{8+64}{2}$ = $\frac{72}{2}$ = 36
As a result, the Arithmetic Mean is 10.
Now, is it possible to include 2 or more numbers in between the 2 numbers given to form the AP?
Assume A₁, A₂, A₃,…, An be n numbers between a and b in a way that a, A₁, A₂, A₃,…, An, b is the A.P.
Here, the number “b” = (n + 2)th term, that is, b = a + [(n + 2) – 1] d = a + (n + 1) d.
This results in the expression:
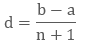
Therefore, “n” numbers in between a & b are the following ones:
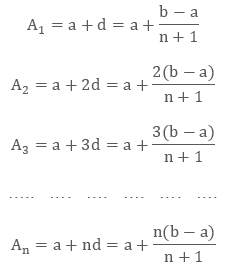
Example
To insert four numbers in between 4 and 20 such that the resulting sequence is an A.P.
Solution:
Let A₁, A₂, A₃, and A be the four numbers between 3 and 18 such that
4, A₁, A₂, A₃, 20 is the given sequence in the A.P.
Here, a = 4, b = 20, n = 5.
Hence,
20 = 4 + (5 –1) d
16 = 4d
d = 4
Therefore, A₁ = a + d = 4 + 4 = 8;
A₂ = a + 2d = 4 + 2 × 4 = 12;
A₃ = a + 3d = 4 + 3 × 4 = 16;
Hence, three numbers in between 4 and 20 are 8, 12, and 16
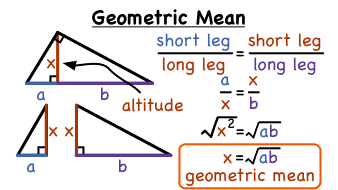
Geometric Mean
Geometric Mean or GM refers to a special average type of the 2 specified numbers. If you are having 2 numbers, then we’ll be multiplying the given numbers and later we’ll be taking the square root (√) of it.
If the two numbers are a & b, then the GM will be given be in the form:
X = √a.b
Example on GM:
Question: What’s the GM of 4 and 64?
Answer:
Given:
a = 4 and b = 64
$\sqrt{464}$
= $\sqrt{256}$
= 16
Here, you can see that the sequence consists of 4,16, 64 which is the GP.
Now,
The Relationship between A.M. and G.M.
As seen above the A.M. & the G.M. formula, which are:
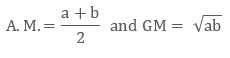
Where,
The 2 +ve numbers are a & b
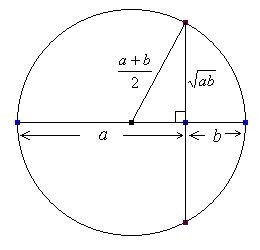
Assuming, A & G as A.M. & G.M. respectively
Therefore,
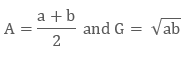
Let’s now do the subtraction of 2 of them
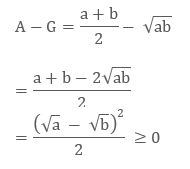
This represents that A ≥ G
Taking the Example
Question: Find the 2 numbers, If Arithmetic mean is 14 and the Geometric mean is 6 of the 2 positive real numbers.
Solution:
Given:
A.M. = $\frac{a+b}{2}$ = 14,
A.M = 28; ………..Eq 1.
G.M. = √a.b
6 = √a.b
a.b = 36………….Eq 2.
Now, putting these values in the numbers a & b in:
(a – b)2 = (a + b)2 – 4ab
(a – b)2 = (28)2 – 4(36)
(a – b)2 = 784 – 144
a – b = ± 80 ( by taking square root) …(3)
By solving (1st) and (3rd), we’ll be getting
a + b = 28
a – b = 80
a = 54, b = -26