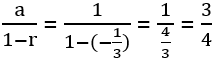Arithmetic and Geometric series infinite G.P. and its sum
If there’s a sequence 10, 20, 30, 40, then each term is 10 more than the earlier term. This is the example of the (AP) Arithmetic Progression & a constant value which clearly describes the difference in between any 2 consecutive terms which is known as the common difference.
If the arithmetic difference consists of ‘a’ as the first term and ‘d’ as the common difference, then you can write the expression as:
The formula is expressed as: (a + d), (a + 2d),… {a + (n-1) d}
Where,
nth term = a + (n−1)d
Arithmetic Series’ Sum
The Arithmetic series’ sum of ‘n’ terms is formed by arranging each n/2 pairs with the sum of 1st and last term’s value.
The formula is as follows:
![]()
Where,
The First term = a;
The Last term = l
While the last term refers to the nth term, i.e. nth term = a + (n − 1)d so we can rewrite it in this form:
![]()
Hence, if the last and first terms are known to you, then you can use the first formula; and use the 2nd formula if common difference and the first term is known to you or are given.
Geometric Progressions (G.P.)
If you have a sequence such as 256, 64, 16, 4, 1, 1/4, 1/16,… then each term is one-third of the term before.
This you can re-write in the form:
(1/4), 81(1/4)², 81(1/3)³, 81(1/3)⁴…
This is the example of the (GP) Geometric Progression, where each term is referred to as the multiple of the earlier one. That particular multiplying factor is known as the common ratio, ‘r’.
Therefore, there’s the Geometric Progression having ‘a’ as the first term & ‘r’ as the common ratio, having n terms. This can be easily stated in the form as follows:
a, ar, ar², ar³, ar⁴…arⁿ⁻¹,
Where nth term = arⁿ⁻¹
Example: In the given sequence of 1200, 600, 300, 150, 75, so, find the 7th term.
Solution: a = 1200, r = 0.5 &
Hence, the 7th term = 1200 × 0.5⁷⁻¹ = 1200 × 0.5⁶
= 1200 * 0.0078125
= 9.375
Hence, the 7th term = 9.375
It’s important to note that for finding out which term contains a specific value which you will require for using logarithms.
Example: In the given sequence, 4, 20, 100, 500… Which is the very first term for exceeding 4,000,000?
Solution: a = 4, r = 5.
4. 5ⁿ⁻¹> 40000000
5ⁿ⁻¹ > 40000000
n − 1) log 5 > log 8000000
n -1 > log 8000000 / log 5 ∵ log 8000000 = 6.9030 & log 5 = 0.6989
∴ n -1 > 6.9030/0.6989
Hence, n -1 > 9.8
n > 10.8
Therefore, n = 11
Sum of Geometric series
Sum of terms can be expressed in 2 different ways:
![]()
Where,
a = first term & r = common ratio; r ≠ 1.
![]()
Note: Use this formula when the value of r < 1
For Example:
Evaluate,
Note: (There are 4 terms)
First term is defined, when n = 3
That is, (1.32)³ = 2.2999
With the use of the formula, G.P’s sum gives:
S₄ = 2.2999 (1.32^4 – 1) / (1.32 – 1)
S₄ = 2.299 (3.0359) / 0.32
S₄ = 6.97 / 0.32
S₄ = 21.81
(Note: there are 9 terms.)
Convergence
Now, Comes, if exist, The sum of the infinite series:
The value of 1 lies in between: -1 < r < 1 or the modulus of the common ratio is less than one, i.e. | r | < 1
This is due to each successive term that gets smaller and smaller and hence, the series will lean towards a specific limit. This particular limit is determined with the use of the 2nd of the 2 formulae:
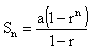
If | r | < 1 next, as n → ∞, rn → 0
And, therefore:
![]()
Example:
Question: The series ¼ + (¼)² + (¼)³ + (¼)⁴ + … when converges & the series’ sum is equal to 1 as n reaches ∞.
Solution:
(The sequence like as n⁴ has the first 6 terms as 1 + 16 + 81 + 128 + 625 + 1292. As the value of ‘n’ reaches ∞ (infinity), then the sum increases too.
Hence, it’s not the convergent any more. This specific series is regarded as the “divergent”.
Every AP consists of the sum which reaches infinity as the value of n accelerates; therefore, every AP is divergent.
Example
Find 1 – 1/3 + 1/9 – 1/27 +…
1 – 1/3 + 1/9 – 1/27 + … = 1 + (-1/3) + (-1/3)² + (-1/3)³ +…
This is the G.P where r = -⅓, therefore, | r | < 1.
Hence, this series has the convergence to or converges to: