Let A and B be two events such that P(B) > 0. Then we can recall that the conditional probability of A given B is:
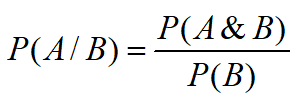
or
Hence, if we are given that event B occurred, the relevant sample space is reduced to B {P(B)=1 because we know B is true} and conditional probability becomes a probability measure on B.
Therefore,
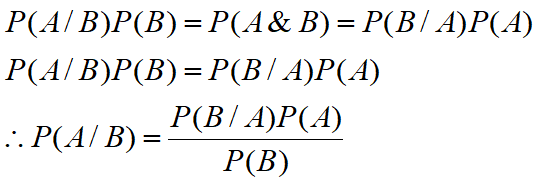
The probability of A given B = probability of B given A X prior probability of A / prior probability of B. This is Baye’s Rule.
Bayes’ Theorem shows the relationship between a conditional probability and its inverse i.e. it allows us to make an inference from the probability of a hypothesis given the evidence to the probability of that evidence given the hypothesis and vice versa
For multiple events:
Given k represents a mutually exclusive and exhaustive event such for B1, B1, . . . Bk, such that P(B1) + P(B2) + … + P(Bk) = 1, where P (B) > 0 and an observed event A, then
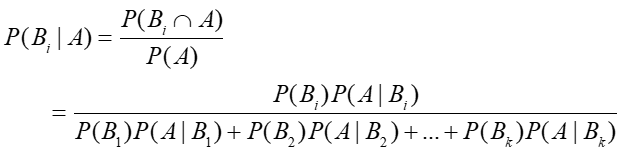
Example: A company manufactures TV at two factories. Factory I produces 60% of the TVs and Factory II produces 40%. Two percent of the TVs produced at Factory I are defective, while 1% of Factory II’s are defective. A TV is selected at random and found to be defective. What is the probability it arrived from Factory I?
Solution
Example: A friend tells you he had a nice conversation with someone on the train to Kerala. What is the chance that this other person is a woman? Your friend only tells you that this person has long hair.
Does this change the previous probability?
Assume that 75% of women have long hair and 15% of men have long hair
Now Let:
- P(W|L) = probability that the person is a woman, given that the person has long hair
- P(W) = the “prior”, the prior probability that the person is a woman
- P(L) = the probability that a person has long hair
- P(L|W) = the probability that a person has long hair given it is a woman
Then:
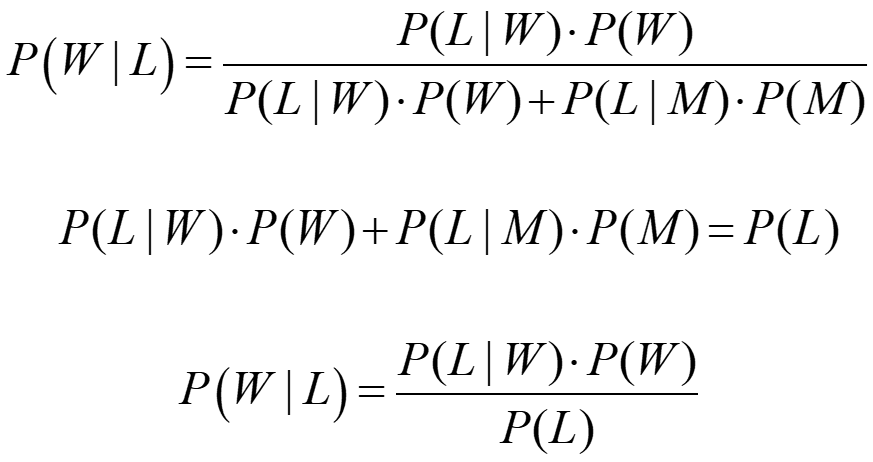
Example: A woman is known to speak truth 2 out of 4 times. She throws a die and reports that it is a 1. Find the probability that it actsually a1.
Solution: Solution Let W be the event that the woman reports that 1 occurs in the throwing of the die and let A be the event that 1 occurs and B be the event that 1 does not occur
Then we know that P(A) = 1/6
And P(B) = 5/6
Then P(W│A) = Probability that the woman reports a 1 occurs when 1 actually occurs = probability that the woman speaks the truth: 2/4 = ½
Now, P(W│B) = Probability that the woman reports that a 1 occurs when 1 does not actually occur = Probability that the woman lies = ½
Then we can use the Bayes theorem for P(A│W) = Probability that the report of the woman that 1 occurs actually occurs.
P(A│W) = $\frac{P(A)P(WA)}{P(A)P(WA)+P(B)P(WB)}=\frac{\frac{1}{6}\times \frac{1}{2}}{\frac{1}{6}\times \frac{1}{2}+\frac{5}{6}\times \frac{1}{2}}=\frac{1}{6}$