Manufacturing problems
In these problems, we determine the number of units of manufacturing products to be produced and sold by a firm. Each product requires fixed manpower, machine time, labour hour per unit of product, warehouse space per unit of the output etc., which can be optimized in order to make maximum profit.
Example: NuGrow makes three different fertilizers which are packaged in 40 lb. bags: 20-10-40, 10-10-10 and 30-30-10 ratio of nitrogen phosphate and potash. The 20-10-40 fertilizer is sold at $8/bag and at least 3000 bags to be produced next month. The 10-10-10 fertilizer is sold at $4/bag. The 30-30-10 fertilizer is sold at $6/bag and at least 4000 bags to be produced next month. The cost and availability of the fertilizer ingredients are as follows:
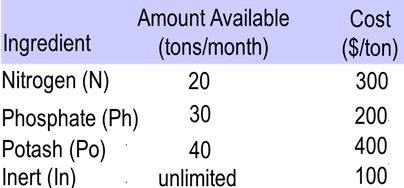
Formulate an LP to find the number of bags of each type of fertilizer NuGrow should make next month to maximize profit.
We can use the table below to summarize the information of 3 products from 4ingredients: 3 variables and 5 constraints.

Here, xi = Number of bags of fertilizer type i to make next month.
i=1: 20-10-40 i=2: 10-10-10 i=3: 30-30-10
Maximize Profit = Revenue – Cost
Revenue = 8x1 + 4x2 + 6x3
Cost = (cost per bag of 20-10-40 ratio) x1
+ (cost per bag of 10-10-10 ratio) x2
+ (cost per bag of 30-30-10 ratio) x3
Cost per bag is the cost of all ingredients in a bag.
Cost for one bag of 20-10-40
= cost for N 8 0.15 ($300/ton=$0.15/lb)
+ cost for Ph 4 0.10 ($200/ton=$0.10/lb)
+ cost for Po 16 0.20 ($400/ton=$0.20/lb)
+ cost for In 12 0.05 ($100/ton=$0.05/lb)
= $5.4
Similarly:
Cost for one bag of 10-10-10 = $3.2
Cost for one bag of 30-30-10 = $4.4
Therefore,
Revenue = 8x1 + 4x2 + 6x3
Cost = 5.4x1 + 3.2x2 + 4.4x3
Maximize 2.6x1 + 0.8x2 + 1.6x3
Subject to
8x1 + 4x2 + 12x3 40000 (N)
4x1 + 4x2 + 12x3 60000 (Ph)
16x1 + 4x2 + 4x3 80000 (Po)
x1 3000 (20-10-40)
x3 4000 (30-30-10)
x1, x2, x3 0
Additional constraints:
1. NuGrow can produce at most 4000 lbs. of 10-10-10 fertilizer next month: x2≤ 100
2. The 20-10-40 fertilizer should be at least 50
Diet problems
In these problems, we determine the number of different kinds of constituents/nutrients which should be included in a diet so as to minimise the cost of the desired diet that contains a minimum amount of each constituent/nutrients.
Example: A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of food P contains 15 units of calcium, 5 units of iron, 6 units of cholesterol and 5 units of vitamin A. Each packet of the same quantity of food Q contains 5 units of calcium, 25 units of iron, 2 units of cholesterol and 2 units of vitamin A. The diet requires atleast 250 units of calcium, atleast 450 units of iron and at most 250 units of cholesterol. How many packets of each food can be used to minimise the amount of vitamin A in the diet and what will then be the minimum amount of vitamin A?
Let x and y be the number of packets of food P and Q respectively where x ≥ 0, y ≥ 0. Mathematical formulation is:
Minimise Z = 5x + 2y (vitamin A)
Subject to
15x + 5y ≥ 250 = 3x + y = 50 (Ca)
5x + 25 y ≥ 450 = x + 5y = 90 (Fe)
6x + 2y ≤ 250 = 3x + y = 125 cholestrol
x ≥ 0, y ≥ 0
Transportation problems
In these problems, we deduce a transportation schedule to find the cheapest and most cost-effective way of transporting a product from factories situated at different locations to destinations.