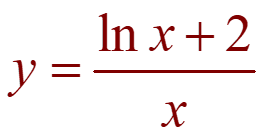Solutions of the linear differential equation of the type − dy/dx + py = q, where p and q are functions of x or constants
A differential equation is called linear if there are no multiplications among dependent variables and their derivatives. In other words, all coefficients are functions of independent variables. It can be written in two forms. The first is discussed in detail here.
$\frac{dy}{dx}+Py=Q$
Such that, P and Q are either constants or functions of x variable only. This type of differential equation is called a first-order linear differential equation. To solve this type of equation, we first multiply both the sides of the equation by a function of x: g(x):
$g(x)\frac{dy}{dx}+P(g(x))y=Qg(x)$
The function $g(x)$ is chosen such that RHS becomes the derivative of y.$g(x)$
Therefore,
$g(x)\frac{dy}{dx}+P(g(x))y=g(x)\frac{dy}{dx}+yg^{‘}(x)$
$P=\frac{g^{‘}(x)}{g(x)}$
Now we integrate both the sides with respect to x to obtain:
$\int{Pdx}=\int{\frac{g^{‘}(x)}{g(x)}}dx$
$\int{Pdx}=\log (g(x))$
Therefore:
$g(x)= e^{\int{P dx}}$
$e^{\int{P dx}}\frac{dy}{dx}+Pe^{\int{P dx}}y=Qe^{\int{P dx}}$
$\frac{d}{dx}(ye^{\int{P dx}})=Qe^{\int{P dx}}$
By integrating both equations we obtain:
$ye^{\int{P dx}}=\int{(Qe^{\int{P dx}})dx}$
$y=e^{-\int{P dx}}\cdot \int{Qe^{\int{P dx}}}dx+C$
Steps used to solve first-order linear differential equation are as follows:
(i) Write the given differential equation in the following first-order linear DE form $\frac{dy}{dx}+Py=Q$
where P, Q are constants or functions of x only.
(ii) Find the Integrating Factor (IF): $e^{\int{P dx}}$
(iii) Write the solution of the given differential equation using IF in the following manner: $y(IF)=\int{(Q\times IF)dx+C}$
Example: y’ – y = e2x
Solution:
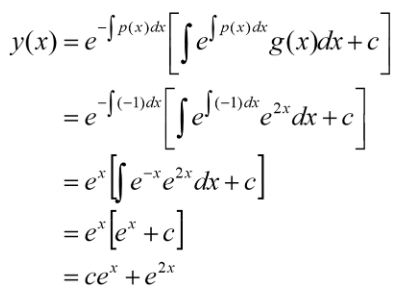
Example: xy’ +2y = x2 – x, y(1) = 1/2
Solution:
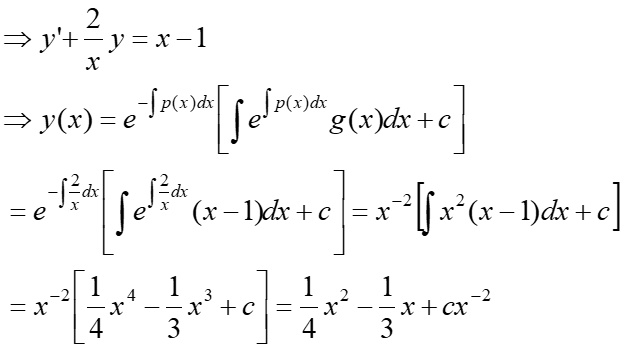
Apply initial condition to obtain c
= $\frac{1}{2}=\frac{1}{4}-\frac{1}{3}+c\to c=\frac{7}{12}$
Example: Solve the differential equation:
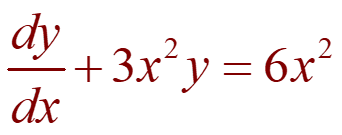
The given equation is a first-order linear DE as it has the form of Equation $\frac{dy}{dx}+Py=Q$
P= 3x2 and Q= 6x2
An integrating factor is:
![]()
Multiplying both sides of the equation by ex3, we get
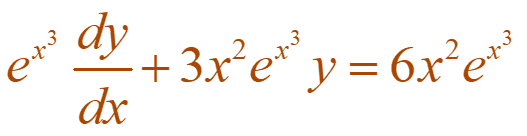
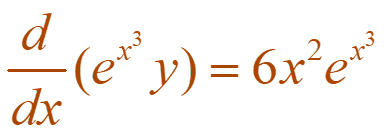
Integrating both sides, we have:
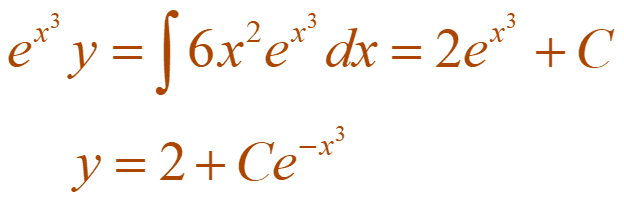
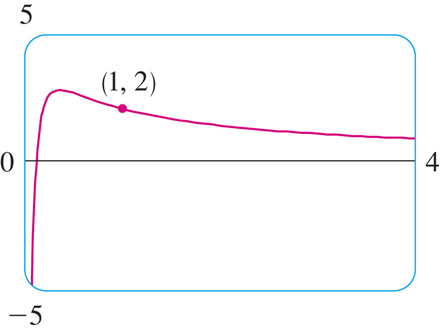
The figure shows the graphs of several members of the family of solutions
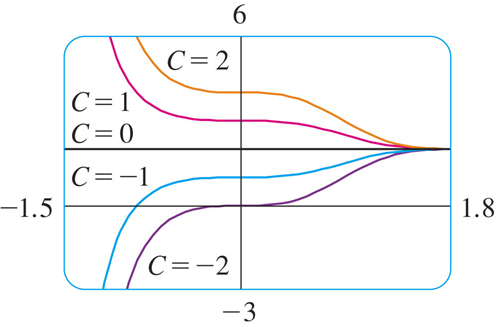
Notice that all the solutions approach 2 as x → .
Example: Find the solution of the initial-value problem: x2y’ + xy = 1 x> 0 y(1) = 2
First, we must divide both sides by the coefficient of y’ to put the differential equation into standard form:
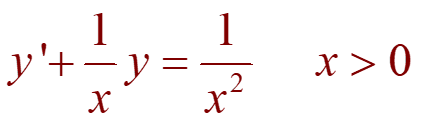
The integrating factor is:
I(x) = e ∫ (1/x) dx = eln x = x
Multiplication of original equation by x gives:
![]()
Therefore,
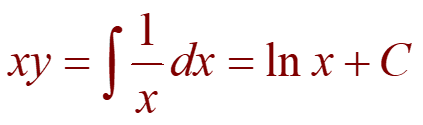
In conclusion:
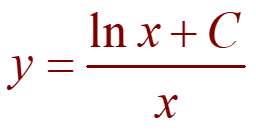
Since y(1) = 2, we have:
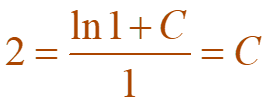
Thus, the solution to the initial-value problem is: