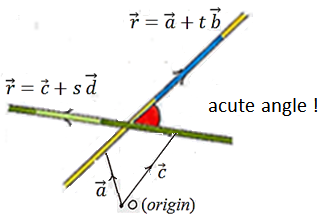
Consider two vectors:
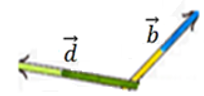
then the acute angle θ between two straight lines is given by:
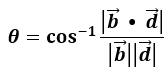
Where b and d can be considered as the direction vectors of the two lines as shown above. The lines do not have to be intersecting – the angle is the angle between them if one was moved along so they do intersect.
In case the lines L1 and L2 do not pass through the origin, we may consider that lines L1’ and L2’are parallel to L1 and L2 respectively and pass them throughthe origin so that these lines have the same equation with different free vector.
Suppose direction cosines of two lines L1 and L2 are given: (l1, m1, n1) and (l2, m2, n2) then we can find the acute angle in the following manner:
$\cos \theta =\vert l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2}\vert $
Note that, two lines containing direction ration a1, b1, c1 and a2, b2, c2 are considered as:
- Perpendicular where θ =90°
Therefore:$a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}=0$ - Parallel where θ =0° $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}
$
Therefore:
Now, let us consider the angle between two lines when their equations are given in the question. If θ is assumed as an acuteangle then the angle between the lines can be written as:
$\overrightarrow{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}$
$\overrightarrow{r}=\overrightarrow{a_{2}}+\lambda \overrightarrow{b_{2}}$
Therefore, in the cartesian form we can write: $\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}$
Also: $\frac{x-x_{2}}{a_{2}}=\frac{y-y_{2}}{b_{2}}=\frac{z-z_{2}}{c_{2}}$
Therefore, to find the acute angle using direction ratio we can write:
$\cos \theta =\vert \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}\cdot \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\vert $
Example: Find the acute angle between the lines with vector equations:
r = (2i + j + k) + t(3i – 8j – k)
and r = (7i + 4j + k) + s(2i + 2j + 3k)
Solution:
$a=(\begin{matrix}
3 & \\
-8 & \\
-1 & \\
\end{matrix}
);b=(\begin{matrix}
2 & \\
2 & \\
3 & \\
\end{matrix}
)$
Calculate the dot product of a and b
$a.b=(\begin{matrix}
3 & \\
-8 & \\
-1 & \\
\end{matrix}
).(\begin{matrix}
2 & \\
2 & \\
3 & \\
\end{matrix}
)$
$a.b=(3\times 2)+(-8\times 2)+(-1\times 3)$
$a.b=-13$
Now calculate the magnitude of a and b:
$\vert a\vert =\sqrt{3^{2}+(-8)^{2}+(-1)^{2}}$
$a|=\sqrt{74}$
$\vert b\vert =\sqrt{2^{2}+2^{2}+3^{2}}$
$|b|=\sqrt{17}$
Substitute the values above to find the angle:
$\cos \theta =\vert \frac{a.b}{\vert a\vert |b|} \vert $
$cos\theta =\vert \frac{-13}{\sqrt{74}\sqrt{17}} \vert $
$cos\theta =\vert -0.3665\ldots \vert $
Since the answer is negative, we need to ‘make it positive’ by multiplying by -1
$cos\theta =0.3665$
$\theta =68.5deg$
Example: Consider the pair of lines given below, find the angle between them.
$\frac{x-3}{3}=\frac{y-1}{5}=\frac{z+3}{4}$
$\frac{x+1}{1}=\frac{y-4}{1}=\frac{z-5}{2}$
Solution: in the cartesian form recall that: $\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}$
The direction ratios of the first line can be seen from the cartesian equation are 3, 5, 4 and for the second line are 1, 1, 2. If θ is the angle between them, they can be written as:
$\cos \theta =\vert \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}\cdot \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\vert $
$\cos \theta =\vert \frac{3\cdot 1+5\cdot 1+4\cdot 2}{\sqrt{3^{2}+5^{2}+4^{2}}\cdot \sqrt{1+1+2^{2}}}\vert =\frac{8\sqrt{3}}{15}$
Hence we can find the required acute angle by taking $\cos ^{-1}\frac{8\sqrt{3}}{15}$