The angle between two planes is considered the same as the angle between their 2 normal vectors as per the geometrical arrangement shown below. These lines are perpendicular to the line of intersection of the planes.
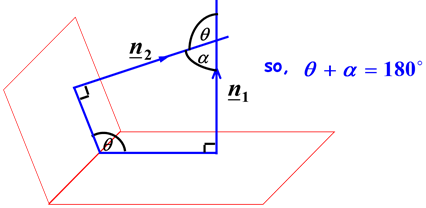
In the figure above, there is a quadrilateral that has 2 angles as shown adding to 180°. So θ + α = 180°
$\cos \theta = \frac{\vert \overrightarrow{n}.\overrightarrow{m}\vert }{\vert \overrightarrow{n}\vert \vert \overrightarrow{m}\vert }$
$\theta =arc cos\frac{\vert \overrightarrow{n}.\overrightarrow{m}\vert }{\vert \overrightarrow{n}\vert \vert \overrightarrow{m}\vert }$
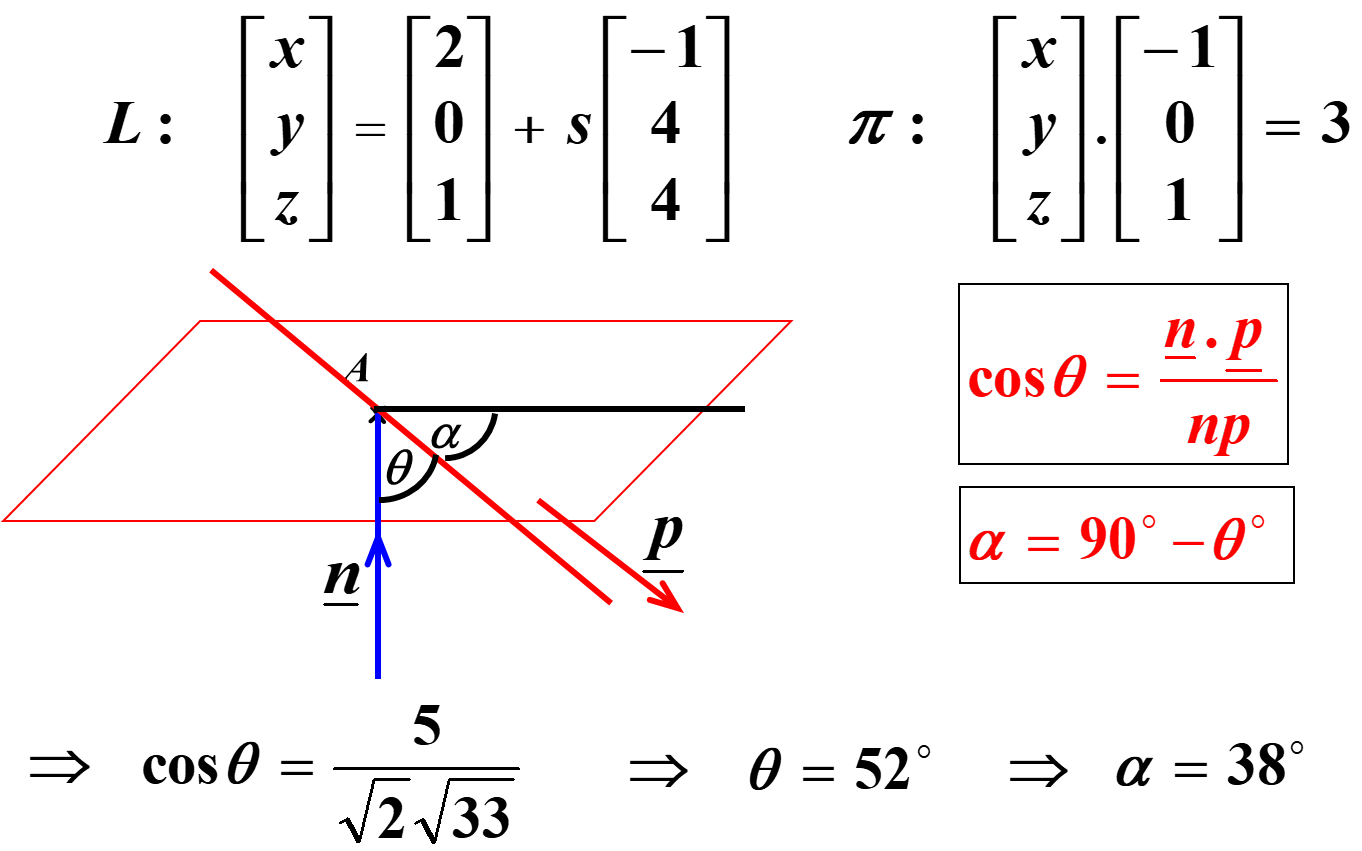
The angle between a line L and a plane p is given by
![]()
Where
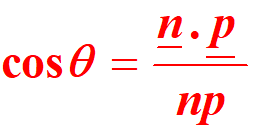
In this case,q is the acute angle between the direction vector of the line,p, and the normal vector to the plane, n. Hence, the angle between 2 planes p1and p2is the angle between their normal vectors and is given by:
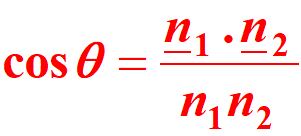
where n1 and n2 denote the normal vectors to the planes under consideration. If necessary subtract from 180° to find the acute angle. Recall that, the planes are perpendicular to each other if n1. n2 = 0 and parallel if n1 is parallel to n2.
We can also write this formula in the cartesian form:
Consider θ to an acute angle between two planes such that:
A1x + B1y + C1z +D = 0 andA2x + B2y + C2z +D = 0 are the equation of the two lines.
The direction ratios of the normal to the planes mentioned above can be written as A1, B1, C1 and A2, B2, C2 respectively.
Therefore, we can use direction ratios to interpret the angle between two normal:
$\cos \theta =\vert \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}\cdot \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\vert $
In a similar format to angles between lines, note that:
1. When the planes are positioned at a right angle to each other, then the normals are perpendicular to each other such that θ =90°. This means that cos θ = 0
Therefore: $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}=0$
2. If the planes are parallel to each other, then the normals are also parallel where θ =0°
Therefore: $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$
Example: Find the angle between planes with the cartesian equation given below:
L1 = 3x – 6y +2z = 7
L2 = 2x + 2y – 2z =5
Solution:
When we compare the equations given above for the planes with the equations
A1 x + B1 y + C1 z + D1 = 0 and A2 x + B2 y + C2 z + D2 = 0 we notice that A1 = 3, B1 = – 6, C1 = 2 and A2 = 2, B2 = 2, C2 = – 2
Now we can substitute the values in the equation to obtain the angle:
$\cos \theta =\vert \frac{3\cdot 2+(-6)\cdot 2+2\cdot (-2)}{\sqrt{3^{2}+(-6)^{2}+(2)^{2}}\cdot \sqrt{2^{2}+2^{2}+(-2)^{2}}}\vert =\frac{5\sqrt{3}}{21}$
$\theta =\cos ^{-1}\frac{5\sqrt{3}}{21}$
Example: Find the angle, to the nearest degree, between the line and plane given below:
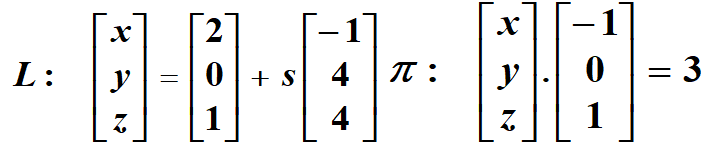
Solution:
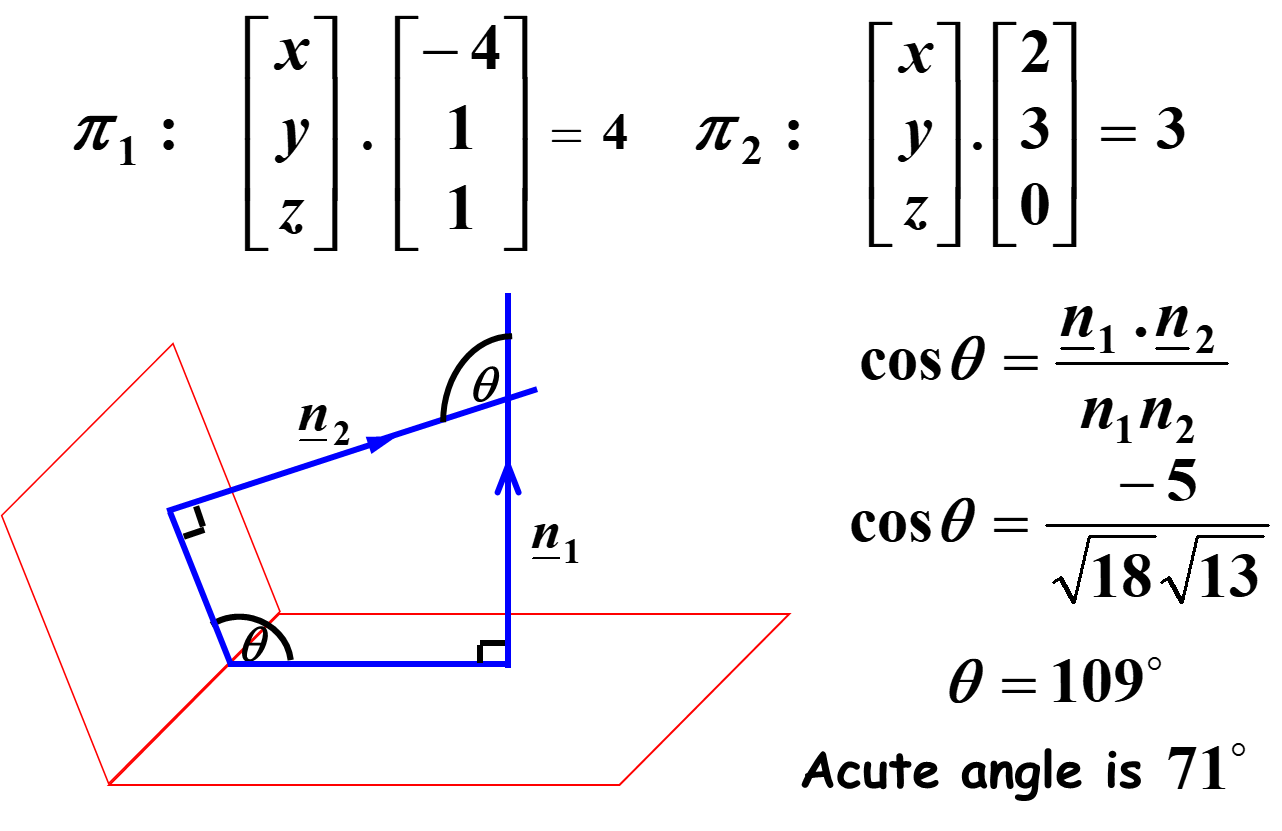
Example: Find the angle, to the nearest degree, between the planes given below:
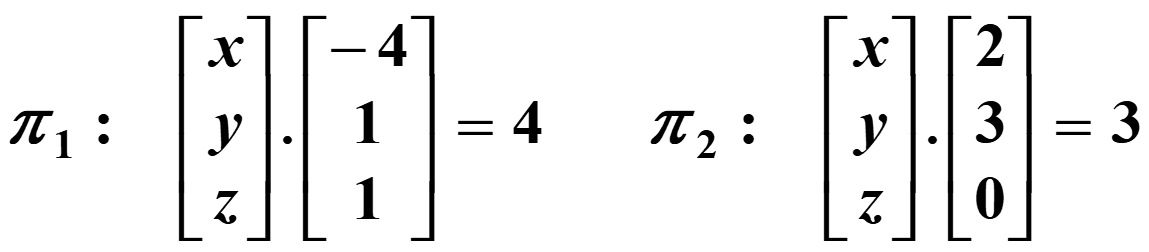
Solution: