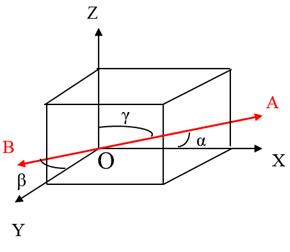
Let a line AB in 3D space make angles α, β, γ respectively with the +ve direction of coordinate axes X, Y, Z. Therefore, we express cosα, cosβ, cosγ as direction cosines of the line AB in the 3D space. Clearly; direction cosines fix the direction cosines of a line in space. Also, parallel lines have the same direction cosines. Direction cosines are denoted by l, m, n respectively. i.e. l = cosα, m = cosβ and n = cosγ. The direction of a line cannot be fixed in space by knowing anyone or any two angles.
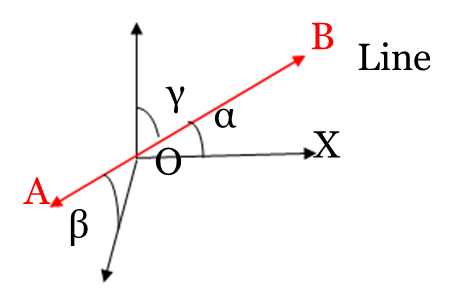
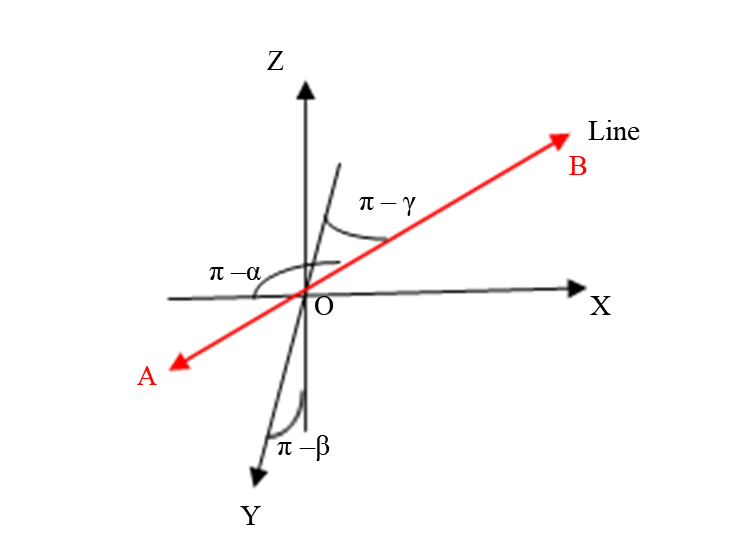
If a line in space makes angles α, β, γ respectively with the +ve direction of X, Y, Z axes then we can assume that the line will make angles π – α, π – β, π – γ with the -ve direction of axes. Therefore, the direction cosines can also be written as cos π -α, cos π -β, cos π –γ. Thus, direction cosines of the same line may also be taken as – cosα, –cosβ, –cosγ.
Three numbers a, b, c proportional to direction cosine l, m, n of a line in space. These numbers are called direction ratios OR direction numbers of the line. Therefore, the direction cosines of a line will be fixed but not the direction ratios:
$\frac{a}{l}=\frac{b}{m}=\frac{c}{n}$
Let direction cosine of any line in space be l, m, n and d.r.’s are a:b:c.Let P(x,y,z) be any point on the line and PM is perpendicular from P on X-axis. Then, in right triangle PMO,
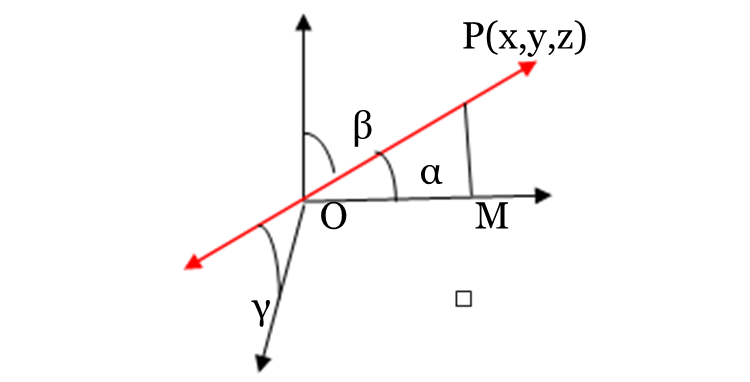
We can see that $\cos \alpha =\frac{OM}{OP}=\frac{x}{r}$ . In this case x = OM and r = OP or $l=\frac{x}{r}$
Similarly, we take the perpendicular point P on y and axis to obtain: $m=\frac{y}{r}; n=\frac{z}{r}$
Hence, we conclude that
$l^{2}+m^{2}+n^{2}=(\frac{x}{r})^{2}+(\frac{y}{r})^{2}+(\frac{z}{r})^{2}$
$=\frac{x^{2}+y^{2}+z^{2}}{r^{2}}=(\frac{r}{r})^{2}=1$
$l^{2}+m^{2}+n^{2}=1$
Recall that $\frac{a}{l}=\frac{b}{m}=\frac{c}{n}$
Then we can elaborate by the properties of ratio and proportion that:
$\frac{a}{l}=\frac{b}{m}=\frac{c}{n}=\frac{\sqrt{a^{2}+b^{2}+c^{2}}}{\sqrt{l^{2}+m^{2}+n^{2}}}=\frac{\sqrt{a^{2}+b^{2}+c^{2}}}{1}$
Hence we can conclude that:
$l=\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}$
$m=\frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}$
$n=\frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}$
To find direction ratio of a line if its two points are known:
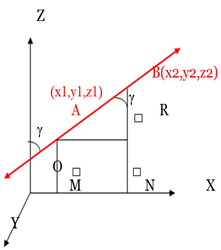
Let AB be a line that is inclined at angles α, β, γ with positive x, y, z-axis at points A (x1, y1, z1) and B at (x2, y2, z2) to form direction ratios. Line AB makes angle γ with the z-axis which is a part of a right angle triangle ∆ARB where,
$n=\cos \gamma =\frac{BR}{AB}=\frac{z_{2}-z_{1}}{AB}$
Also,
$l=\cos \alpha =\frac{x_{2}-x_{1}}{AB}$
$m=\cos \beta =\frac{y_{2}-y_{1}}{AB}$
Therefore, l:m:n = $\frac{x_{2}-x_{1}}{AB}, \frac{y_{2}-y_{1}}{AB},\frac{z_{2}-z_{1}}{AB}$= $(x_{2}-x_{1}), (y_{2}-y_{1}), (z_{2}-z_{1})$