Definition, Geometrical Interpretation, properties and application of scalar (dot) product of vectors, vector (cross) product of vectors, a scalar triple product of vectors
The dot/scalar product of two vectors $\overrightarrow{a}$and $\overrightarrow{b}$ is:$\overrightarrow{a}. \overrightarrow{b}= \overrightarrow{b} . \overrightarrow{a} =\vert \overrightarrow{a}\vert \vert \overrightarrow{b}\vert \cos \theta $
It is essentially the product of the length of one of them and projection of the other one on the first one:


Let: $\overrightarrow{a}=(\begin{matrix}
a_{x} & \\
a_{y} & \\
a_{z} & \\
\end{matrix}
)$ and $\overrightarrow{b}=(\begin{matrix}
b_{x} & \\
b_{y} & \\
b_{z} & \\
\end{matrix}
)$, ${i} .{i} =1 {j}.{j}=1 {k}.{k}=1 {i}.{j}=0 {i}.{k}=0 {j}.{k}=0 (\cos 90^{0}=0)$
Then,
$\overrightarrow{a} . \overrightarrow{b}=(a_{x}{i} + a_{y}{j} + a_{z}{k}).(b_{x}{i} + b_{y}{j} + b_{z}{k})$=$ \overrightarrow{a} . \overrightarrow{b}=(\begin{matrix}
a_{x} & \\
a_{y} & \\
a_{z} & \\
\end{matrix}
)(\begin{matrix}
b_{x} & \\
b_{y} & \\
b_{z} & \\
\end{matrix}
)=a_{x}b_{x}+a_{y}b_{y}+a_{z}b_{z}$
Properties of dot product:
$ \overrightarrow{a} . \overrightarrow{b}= \overrightarrow{b} . \overrightarrow{a}$
if $\overrightarrow{a}$ and $\overrightarrow{b}$ are vectors that are parallel to each other, then $\overrightarrow{a} . \overrightarrow{b}= \vert \overrightarrow{a}\vert \vert \overrightarrow{b}\vert$
if $\overrightarrow{a}$ and $\overrightarrow{b}$ are vectors that are antiparallel to each other, then $\overrightarrow{a} . \overrightarrow{b}=- \vert \overrightarrow{a}\vert \vert \overrightarrow{b}\vert$
$ \overrightarrow{a} . \overrightarrow{a}= \vert \overrightarrow{a} \vert ^{2}$
$\overrightarrow{a} .(\overrightarrow{b} + \overrightarrow{c})=\overrightarrow{a}.\overrightarrow{b} + \overrightarrow{a}.\overrightarrow{c}$
$(\overrightarrow{a}+\overrightarrow{b}) .(\overrightarrow{c}+\overrightarrow{d})=\overrightarrow{a}.\overrightarrow{c} + \overrightarrow{a}.\overrightarrow{d}+\overrightarrow{b}.\overrightarrow{c} + \overrightarrow{b}.\overrightarrow{d}$
$\overrightarrow{a} . \overrightarrow{b}=0 (\overrightarrow{a} \ne 0, \overrightarrow{b}\ne 0) \leftrightarrow \overrightarrow{a} and \overrightarrow{b}$ are perpendicular.
Cross product:
$\vert \overrightarrow{p} \times \overrightarrow{q}\vert = \vert \overrightarrow{p}\vert \vert \overrightarrow{q}\vert sin \theta$
The magnitude of the vector $\overrightarrow{p}\times \overrightarrow{q}$ is equal to the area determined by both vectors. The direction of the vector $\overrightarrow{p}\times \overrightarrow{q}$ is given by right-hand rule:
Point the fingers in the direction of $\overrightarrow{a}$; curl them toward $\overrightarrow{b}$. The thumb shall then point in the direction of the cross product.
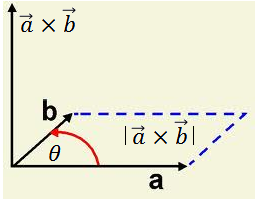
Note that: $\overrightarrow{b}\times \overrightarrow{a}=-\overrightarrow{a} \times \overrightarrow{b}$
In cartesian coordinates:
Using properties of determinates:
$\vert \begin{matrix}
a & b & \\
c & d & \\
\end{matrix}
\vert =ad-cb$
We can write the cross product in simple form:
$\overrightarrow{a} \times \overrightarrow{b}= \vert
\begin{matrix}
{i} & {j} & {k} & \\
a_{x} & a_{y} & a_{z} & \\
b_{x} & b_{y} & b_{z} & \\
\end{matrix}
\vert $
$={i} \vert \begin{matrix}
a_{y} & a_{z} & \\
b_{y} & b_{z} & \\
\end{matrix}
\vert -{j}\vert \begin{matrix}
a_{x} & a_{z} & \\
b_{x} & b_{z} & \\
\end{matrix}
\vert +{k}\vert \begin{matrix}
a_{x} & a_{y} & \\
b_{x} & b_{y} & \\
\end{matrix}
\vert =(\begin{matrix}
a_{y}b_{z}-a_{z}b_{y} & \\
a_{z}b_{x}-a_{x}b_{z} & \\
a_{x}b_{y}-a_{y}b_{x} & \\
\end{matrix}
)$
Properties of cross product:
$\overrightarrow{p} \times \overrightarrow{q}=- \overrightarrow{q} \times \overrightarrow{p}$
$if \overrightarrow{p} and \overrightarrow{q} are perpendicular, then \vert \overrightarrow{p} \times \overrightarrow{q}\vert = \vert \overrightarrow{p}\vert \vert \overrightarrow{q}\vert $
$\overrightarrow{p} \times (\overrightarrow{q} + \overrightarrow{r})=\overrightarrow{p}\times \overrightarrow{q} + \overrightarrow{p}\times \overrightarrow{r}$
$(\overrightarrow{p}+\overrightarrow{q}) \times (\overrightarrow{r}+\overrightarrow{s})=\overrightarrow{p}\times \overrightarrow{r} + \overrightarrow{p}\times \overrightarrow{s}+\overrightarrow{q}\times \overrightarrow{r} + \overrightarrow{q}\times \overrightarrow{s}$
$\overrightarrow{p} \times \overrightarrow{q}= 0 (\overrightarrow{p} \ne 0, \overrightarrow{q}\ne 0) \leftrightarrow \overrightarrow{a} and \overrightarrow{b} are parallel$
$For parallel vectors, the vector product is always 0$
Example:
$\overrightarrow{a} = 5{i}-2{j} +{k}$
$\overrightarrow{b} = {i}+{j}-3{k}$
(a) Find the angle between them
(b) Find the unit vector perpendicular to both
(a) $\theta =arc sin\frac{\vert \overrightarrow{a} \times \overrightarrow{b}\vert }{\vert \overrightarrow{a}\vert \vert \overrightarrow{b}\vert }$
$\overrightarrow{a} \times \overrightarrow{b}=\vert \begin{matrix}
{i} & {j} & {k} & \\
5 & -2 & 1 & \\
1 & 1 & -3 & \\
\end{matrix}
\vert = 5{i}+16{j}+7{k}$
$ \vert \overrightarrow{a} \times \overrightarrow{b}\vert =\vert
5{i}+16{j}+7{k}\vert =\sqrt{330}$
$ \vert \overrightarrow{a} \vert =\sqrt{30} \vert
\overrightarrow{b} \vert =\sqrt{11}$
$\theta =arc sin 1 = \pi /2$
(b) ${n}=\frac{\overrightarrow{a} \times \overrightarrow{b}}{\vert
\overrightarrow{a} \times \overrightarrow{b}\vert }$ = $\frac{1}{\sqrt{330}}(\begin{matrix}
5 & \\
16 & \\
7 & \\
\end{matrix}
)$
Example:
Find all vectors perpendicular to both
$\overrightarrow{a}=(\begin{matrix}
1 & \\
2 & \\
3 & \\
\end{matrix}
) and \overrightarrow{b}=(\begin{matrix}
3 & \\
2 & \\
1 & \\
\end{matrix}
)$
$\overrightarrow{a}\times \overrightarrow{b}=\vert \begin{matrix}
{i} & {j} & {k} & \\
1 & 2 & 3 & \\
3 & 2 & 1 & \\
\end{matrix}
\vert =(\begin{matrix}
-4 & \\
8 & \\
-4 & \\
\end{matrix}
)$
⤇ vector of the form $k({i}-2{j}+{k})$
where k is any non-zero real number.
Example:
Find the area of the triangle with vertices A(1,1,3), B(4,-1,1), and C(0,1,8)
The triangle is½ the area of the parallelogram determined by the vectors given below:
$\overrightarrow{AB}=(\begin{matrix}
3 & \\
-2 & \\
-2 & \\
\end{matrix}
)$ and $\overrightarrow{AC}=(\begin{matrix}
-1 & \\
0 & \\
5 & \\
\end{matrix}
)$
$\frac{1}{2}\vert \overrightarrow{AB}\times \overrightarrow{BC}\vert
=\frac{1}{2}\vert \vert \begin{matrix}
{i} & {j} & {k} & \\
3 & -2 & -2 & \\
-1 & 0 & 5 & \\
\end{matrix}
\vert \vert ⤇ \frac{1}{2} \vert (\begin{matrix}
-10 & \\
-13 & \\
-2 & \\
\end{matrix}
)\vert =\frac{1}{2} \sqrt{(-10)^{2}+(-13)^{2}+(-2)^{2}}$
$=8.26 units^{2}$
Volume of a parallelepiped = scalar triple product
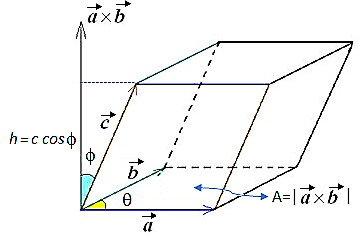
$V=\vert \overrightarrow{c} ⤇ ( \overrightarrow{a} \times
\overrightarrow{b})\vert =\Vert \begin{matrix}
c_{x} & c_{y} & c_{z} & \\
a_{x} & a_{y} & a_{z} & \\
b_{x} & b_{y} & b_{z} & \\
\end{matrix}
\Vert units^{3}$
The volume of a tetrahedron = $\frac{1}{6}$ scalar triple product
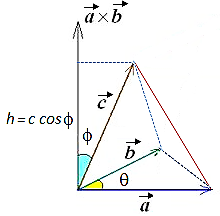
$V=\frac{1}{6}\vert \overrightarrow{c} ⤇ ( \overrightarrow{a} \times
\overrightarrow{b})\vert =\frac{1}{6} \Vert \begin{matrix}
c_{x} & c_{y} & c_{z} & \\
a_{x} & a_{y} & a_{z} & \\
b_{x} & b_{y} & b_{z} & \\
\end{matrix}
\Vert units^{3}$
Any 4 points are coplanar if the volume of the tetrahedron = 0
Example:Are the points A(1, 2, -4), B(3, 2, 0), C(2, 5, 1) and D(5, -3, -1) coplanar?
$\overrightarrow{AB}=(\begin{matrix}
2 & \\
0 & \\
4 & \\
\end{matrix}
) \overrightarrow{AC}=(\begin{matrix}
1 & \\
3 & \\
5 & \\
\end{matrix}
) \overrightarrow{AD}=(\begin{matrix}
4 & \\
-5 & \\
3 & \\
\end{matrix}
) $
⤇
$\overrightarrow{AB} . \lbrack \overrightarrow{AC}\times
\overrightarrow{AD}\rbrack =\vert \begin{matrix}
2 & 0 & 4 & \\
1 & 3 & 5 & \\
4 & -5 & 3 & \\
\end{matrix}
\vert =2(9+25)+4(-5-12)=0$
∴ A, B, C and D are coplanar Q.E.D