Consider that we are given a point Q, not in a plane and a point P on the plane and our goal for the question is to find the shortest distance possible between the point Q and the plane. The shortest distance between any two points is at a perpendicular state. The distance between a plane and a point Q that is not on the plane can be found by projecting the vector $\overrightarrow{PQ}$ onto the normal vector n (calculating the scalar projection $proj_{n}\overrightarrow{PQ}$), we can find the distance D as shown below:
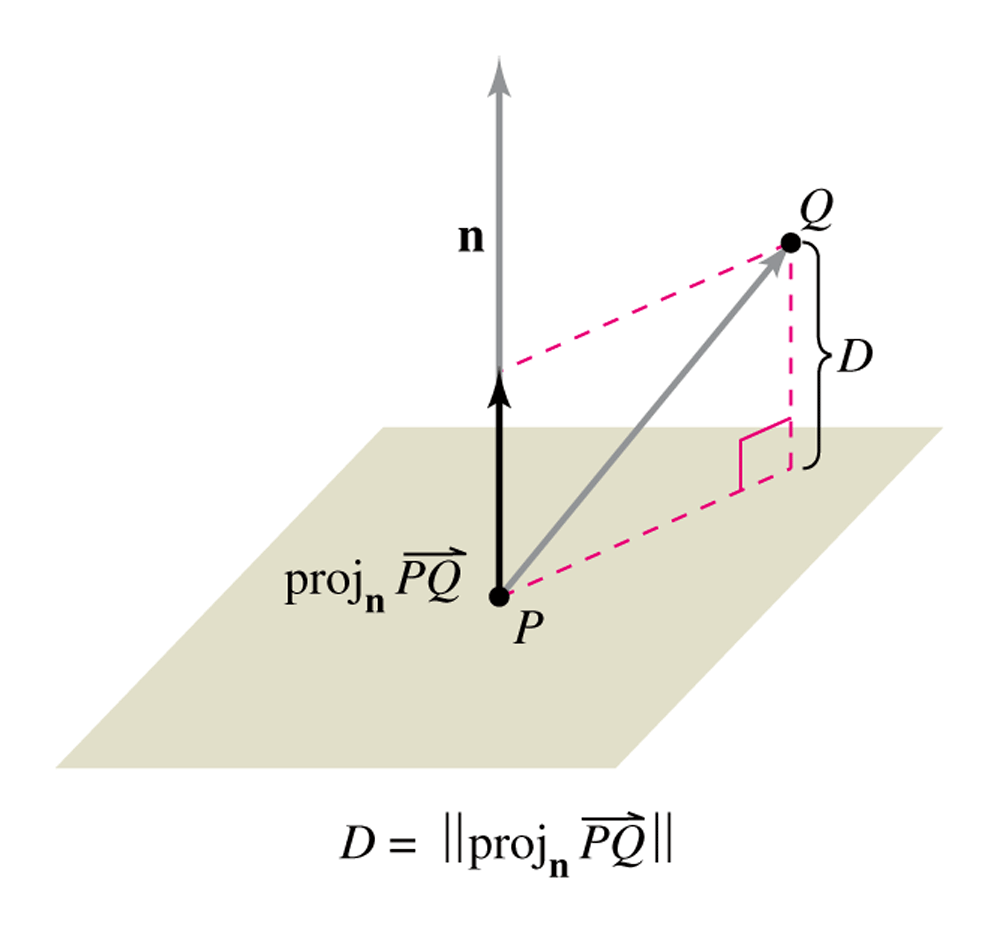
$D=\frac{\Vert \overrightarrow{PQ}\cdot \overrightarrow{n}\Vert }{\Vert \overrightarrow{n}\Vert }$
In this case, P is a point in the plane while is n is normal to the plane. If the equation of the plane is $r\cdot {n}=d$, then $d$ the shortest distance between the origin and a point on the plane.
Example:Find a formula for the distance D from a point P1(x1, y1, z1) to the plane with standard equation ax + by + cz + d = 0.
Consider a point P0(x0, y0, z0) to be any point in the plane. Now let b to be the vector for line segment $\overrightarrow{P_{0}P_{1}}$.
Then, b = <x1 – x0, y1 – y0, z1 – z0>. Notice that the distance D from P1 to the plane is equal to the absolute value of the scalar projection of b onto the normal vector n = <a, b, c>.
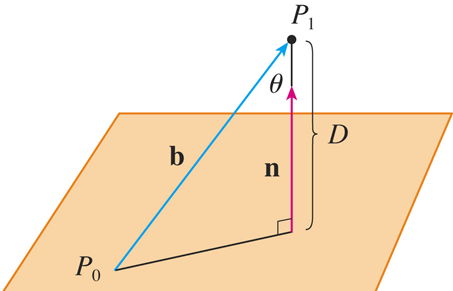
Thus, $D= proj_{n}\overrightarrow{b}$
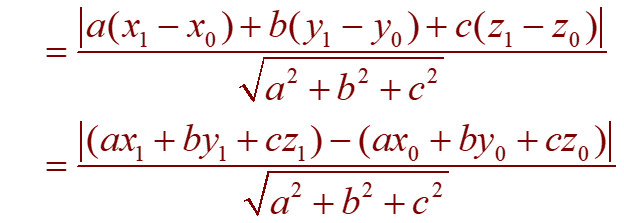
Since P0 lies in the plane under consideration, the coordinates that we deduced satisfy the equation of the plane.Thus, we have ax0 + by0 + cz0 + d = 0.Hence, the formula for D can be written as:
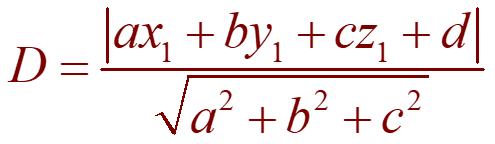
Example:Find the distance between the parallel planes 10x + 2y – 2z = 5 and 5x + y – z = 1
Solution: First, we note that the planes are parallel because their normal vectors <10, 2, –2> and <5, 1, –1> are parallel to each other.To find the distance D between the planes, we deduce any point on one plane and then use that point calculate its distance to the other plane.
In particular, if we put y = z =0 in the equation of the first plane, we get 10x = 5.So, (½, 0, 0) is a point that lies on this plane and satisfies both conditions. Therefore, the distance between (½, 0, 0) and the plane 5x + y – z – 1 = 0 is:
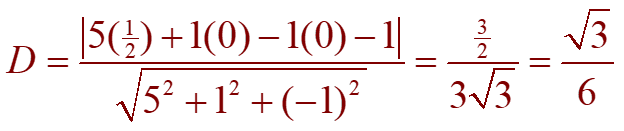
So, the distance between the planes is $\frac{\sqrt{3}}{6}$.