The angle between a line, d, and a plane, π, is the angle between d and its orthogonal projection onto π, d’. Accordingly, the angle between a line and a plane can be considered equivalent to the complementary acute angle that forms between the direction vector of the line $\overrightarrow{d}=(a_{2}, b_{2},c_{2})$ and the normal vector, $\overrightarrow{n}=(a_{1}, b_{1},c_{1})$ of the plane.
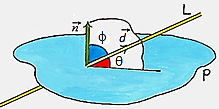
From the formula of the scalar product of vectors find the cosine of the angle between the normal vector and direction vector we can conclude that:
Φ is considered as the angle between the line and the plane which is the complement of θ or 90 – θ as shown in the figure above. Recall that, cos θ = sin (90 – θ). So Φ can be given by:
sin (90 – θ) = cos θ
or
$\sin \theta =\cos \varphi = \frac{\vert \overrightarrow{n}.\overrightarrow{d}\vert }{\vert \overrightarrow{n}\vert \vert \overrightarrow{d}\vert }$
$\theta =arc sin \frac{\vert \overrightarrow{n}.\overrightarrow{d}\vert }{\vert \overrightarrow{n}\vert \vert \overrightarrow{d}\vert }$
In the cartesian form the angle between this line and plane can be found using this formula:
$\sin \theta =\vert \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}\cdot \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\vert $
If the line, $\overrightarrow{d}$, and the plane, π, are perpendicular, the direction vector of the line and the normal vector of the plane have the same direction and therefore its components are proportional:
Therefore: $\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$
Example: Find the angle between the line and plane given below:
Line: $\frac{x-4}{2},\frac{y+2}{6}, \frac{z-6}{-3}$
Plane: x – 2y + 3z + 4 = 0
Solution: Consider θ to be the angle between the line and the normal to the plane.
From the equation of the line, we find the direction vector as $\overrightarrow{d}=(2, 6, -3)$
From the equation of the plane, we find the normal vector as $\overrightarrow{n}=(1, -2, 3)$
Now we can use the equation discussed before to find the angle between the line and the plane:
$\sin \theta =\vert \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}\cdot \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\vert $
$\sin \theta =\vert \frac{2\cdot 1+6\cdot (-2)+(-3)\cdot 3}{\sqrt{2^{2}+6^{2}+(-3)^{2}}\cdot \sqrt{1^{2}+(-2)^{2}+3^{2}}}\vert =\frac{19}{7\sqrt{14}}$
Therefore, we can find the angle as: $\theta =\sin ^{-1}\frac{19}{7\sqrt{14}}$
Example: Determine the angle between the line and the plane given below:
Line: $r=\bigg\{
\begin{gathered}
y=2 \\
3x-\sqrt{3}z=0 \\
\end{gathered}
$
Plane: x=1
Solution
We can also write line r as: $r=\bigg\{
\begin{gathered}
x= \sqrt{3}\lambda \\
y=2 \\
z=3\lambda \\
\end{gathered}
$
Hence, we can obtain the direction vector as $\overrightarrow{r}=(\sqrt{3},0, 3)$ and normal vector $\overrightarrow{n}=(1, 0, 0)$
Now, we can substitute the values to obtain the angle between the direction vector and the normal vector:
$\sin \theta =\vert \frac{\sqrt{3}\cdot 1+0\cdot 0+3\cdot 0}{\sqrt{\sqrt{3}^{2}+0^{2}+3^{2}}\cdot \sqrt{1^{2}+0^{2}+0^{2}}}\vert =\frac{1}{2}$
$\sin ^{-1}\theta =30 degrees$
Example: Find the coordinates of the point where the line through the points
A (3, 4, 1) and B(5, 1, 6) crosses through the XY-plane.
Solution: The vector equation of the line through points A and B is
$\overrightarrow{r}=3i+4j+k+\lambda [(5-3)i+(1-4)j+(6-1)k]$
$\overrightarrow{r}=3i+4j+k+\lambda [2i-3j+5k]$
Consider P to be the point where the line AB crosses through the XY-plane. Then the position
vector of the point P is of the form xi + yj. Hence we can write:
$xi+yj=(3+2\lambda )i+(4-3\lambda )j+(1+5\lambda )k$
Now we equate to solve for x, y, and z
$x=(3+2\lambda )$
$y=(4-3\lambda )$
$0=(1+5\lambda )$
Hence, the coordinates for the equations are: $(\frac{13}{5},\frac{23}{5}, 0)$