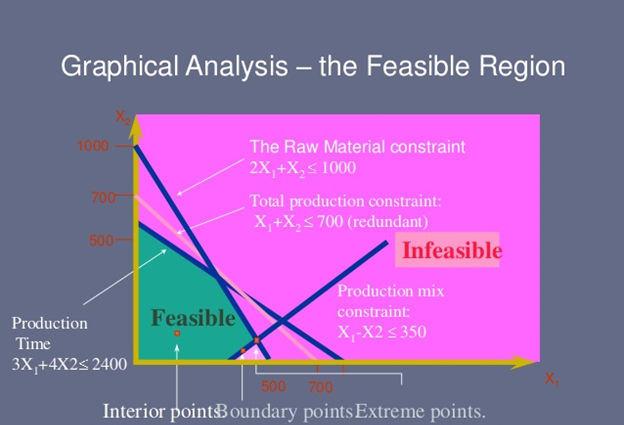
Feasible and infeasible regions (bounded and unbounded)
For a standard maximum/minimum problem a range of values is said to be feasible if they satisfy the corresponding constraints.The set of feasible vectors is called the constraint set which lies on the feasible regions.So, if the constraint set is not empty, then the LP is feasible or else it is said to be infeasible.A feasible maximum (resp. minimum) problem is said to be unbounded if the objective function has arbitrarily large positive (resp. negative) values at feasible vectors; otherwise, it is said to be in the bounded region.
There are three possibilities for a linear programming problem: bounded feasible, unbounded feasible, and infeasible.In real life, we often face situations in which it is impossible to satisfy all the restrictions confronting us. For example, suppose Healthy Pet Food wanted to supply at least 160,000 packages of dog food each month; that is M+Y≥ 160,000. No points satisfy the original constraints and M + Y ≥ 160,000 simultaneously. Identifying this situation is useful because we can then identify which constraints might be relaxed to obtain a feasible solution and what the consequences of relaxing the constraints will be.The value of a bounded feasible maximum (resp, minimum) problem is the maximum(resp. minimum) value of the objective function. This is possible because the constraint variables range over the constraint set. Sometimes a linear program has an unbounded solution. Likewise, the objective function obtains a value of positive infinity for a maximization problem or negative infinity for a minimization problem. For example, consider the problem:
Maximize z = A + 2B
Subject to
A ≤ 10
2A B ≥ 5
A, B ≥ 0
As long as A is kept less than or equal to 10, B can be increased without limit and the objective function increases without limit. There is no finite optimum. Unboundedness explains the objective function value, not the constraint set. It is true that for the objective function to be unbounded the feasible region must be unbounded in some direction. However, an unbounded feasible set does not imply that there is no finite optimum. To see this, we simply have to change the objective of the preceding example to minimize A + 2B. The feasible set is unaffected, and therefore still unbounded in some direction. However, the optimal solution is (A = 2.5, B= 0, z = 2.5).
Although infeasible problems can occur in practice, an unbounded problem generally indicates misrepresentation of one or more constraints. When an unbounded problem is encountered, the analyst should study the situation to see what limitations exist that are not being explicitly stated in the constraints.