A normal to a line is considered as a line segment drawn from a point that is perpendicular to the given line.
The normal form of a linear equation of a straight line uses two parameters: p and α to describe the line. Here, p stands for the length of the perpendicular from the origin to the line. And α is the angle between this perpendicular and the x-axis. Let p be the length of the normal drawn from the origin to a line, which subtends an angle α with the +I ve direction of the x-axis as follows. Consider the graph below where p is the length of a perpendicular from origin to the non-vertical line l and α is the inclination of p, then show that the equation of the line is
$x\cos \alpha +y\sin \alpha =p $
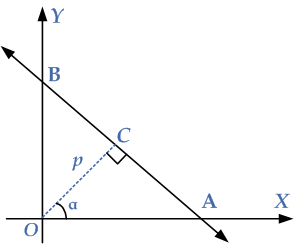
To prove this equation of a straight line is in normal form, consider P(x,y) be any point on the straight line l. Since the line intersects the coordinate axes at points A and B, then OA and OB become its X-intercept and Y-intercept. Now using the equation of a straight line intercepts form, we have
$\frac{x}{OA}+\frac{y}{OB}=1$
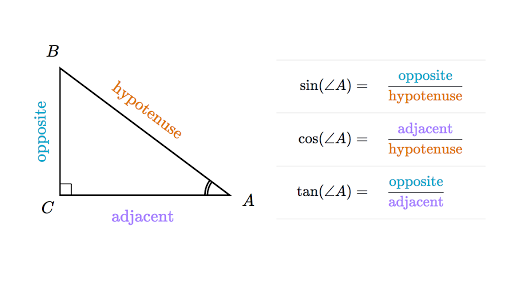
If C is the foot of the perpendicular drawn from origin O to the non-vertical straight line, then consider OCA is the right triangle as given in the diagram. Use the trigonometric ratios to obtain:
$\frac{OC}{OA}=\cos \alpha $
$\frac{P}{OA}=\cos \alpha $
This means that OC =p
Since OCB is a right triangle, then OCOB=cos(90°−α)
$\frac{P}{OB}=\sin \alpha $
Now put the values of OA and OB in the equation above, we get:
$\frac{x/p}{cos\alpha }+\frac{y/p}{sin\alpha }=1$
$x\cos \alpha +y\sin \alpha =p$
This form of the equation is called the normal form.
To convert the general equation of a line into the normal form:
Begin with the general or linear form of the straight line equation:
ax+by+c=0
From the above equations, we obtain:
Cos α = p/m and Sin α = p/n
From Trigonometric identity, we have
Cos2α + Sin2α =1
$\frac{p^{2}}{m^{2}}+\frac{p^{2}}{n^{2}}=1$
Simplifying this equation gives:
$P=\frac{mn}{\sqrt{m^{2}+n^{2}}}$
Since P is the perpendicular distance from the origin to the line, we get:
$ax+by=0; \vert c\vert /\sqrt{a^{2}+b^{2}}$
Therefore, we convert the linear equation by diving it by the factor of $\sqrt{a^{2}+b^{2}}$
Hence, we obtain the following equation:
$
\frac{a}{\sqrt{a^{2}+b^{2}}}x+\frac{b}{\sqrt{a^{2}+b^{2}}}y+\frac{c}{\sqrt{a^{2}+b^{2}}}=0
$
Recall the trigonometric identity: Cos2α + Sin2α =1 and the trigonometric ratios:
$\frac{a}{\sqrt{a^{2}+b^{2}}}=\cos \alpha $
$\frac{b}{\sqrt{a^{2}+b^{2}}}y=\sin \alpha $
$\frac{c}{\sqrt{a^{2}+b^{2}}}=p$
Substituting the values, we obtain:
$x\cos \alpha +y\sin \alpha =p$
Distance between a point and a line:
Consider the graph below
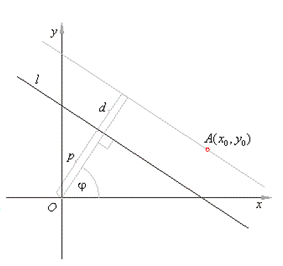
The distance from point A to a line l is equal to the distance between the given line and the parallel line passing through point A. This means that the length p+d and coordinates of A are sufficient to obtain the line equation:
$x_{0}cos\phi + y_{0}sin\phi =p+d$
$d=x_{0}cos\phi + y_{0}sin\phi -p$