An equation of a line can be written as a linear equation in slope-intercept form y = mx + b. Here, m is the slope and b is the y-intercept. The y-intercept is known as a point where a line crosses the y-axis.
Example 1. Write an equation in slope-intercept form of the line that has a slope of 5 and a y-intercept of 8.
To write an equation, you need two things:
slope (m) = 5
y – intercept (b) = 8
Plug them into slope-intercept form
y = mx + b
y = 5x + 8
Example 2. When given an equation, you can easily graph it in slope-intercept form by deducing two things– the slope (m) and y-intercept (b).
Make sure the equation is in slope-intercept form
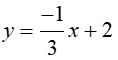
Find the slope and y-intercept
Start by graphing the y-intercept (b = 2).
Plot the y-intercept on the graph as shown below
Apply the slope (rise/run) to the y-intercept by using the y-intercept, and apply “rise over run” using your slope where rise = 1, run = -3
Repeat this again from your new point. Draw a line through your points.
Example 2. Write the Equation of a Line from the graph given below.
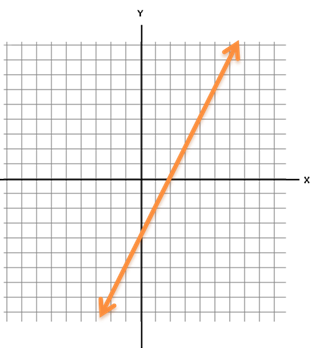
Where does the line cross the y-axis?
- Notice the point (0, -4) on the graph above, the y-intercept is -4.
What is the slope of the line?
- The graph also crosses the x-axis at (2, 0) which is the x-intercept
- Using the slope formula to find our slope. $m=\frac{-4-0}{0-2}=\frac{-4}{-2}=2$
We know, m= 2 and b= -4, what is the equation of our line?
y = mx + b
y = 2x + (-4)
y = 2x -4
Example 3. Find the slope and y-intercept for 2y + 2 = 4x
2y + 2 = 4x
2y = 4x – 2
y = 2x – 1
m =2 and b = -1
Example 4. A line with a slope of -3 and it passes through the point (1, 2). Find the equation.
y = mx + b
$2=-3(1)+b$
b = 5
y = -3x + 5
Example 5. Find the equation of a line that passes through the points (-2, 1) and (4, 2).
To write an equation, you need two things: slope (m) and y-intercept (b)
First, we have to find the slope. Plug the points into the slope formula.
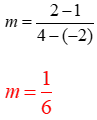
Pick one of the ordered pairs, (4, 2) and plug into the equation $2=\frac{1}{6}(4)+b$
Solve the equation for b.
b = 4/3
Now substitute values for m and b
![]()