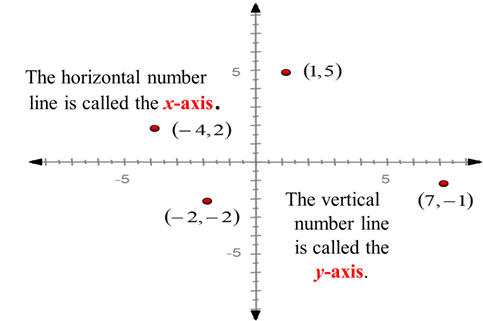
Figure 1: The coordinate plane.
Cartesian coordinates
In mathematics, a plane is defined as a flat infinite surface that spreads forever in every direction. In Algebra, we often use the coordinate plane which is divided by two number lines. The horizontal line is x-axis with negative points in the left of the origin and positive points on the right. As for the vertical line or y-axis, the points above the origin are positive and the bottom is the negative points on the coordinate plane. The origin is known as the point where the two number lines meet and the coordinates act like an address of the points from the origin. Coordinates are always written by using parentheses for the x and y points. The x-value first, then y and z in an ordered pair.


The two number lines divide the plane into four regions called quadrants which are labelled with roman numerals.

Distance between two points
The Distance formula is used to deduce the distance between to different given points on a graph. The distance d between any two points with the coordinates (x1,y1) and (x2,y2) is given by:
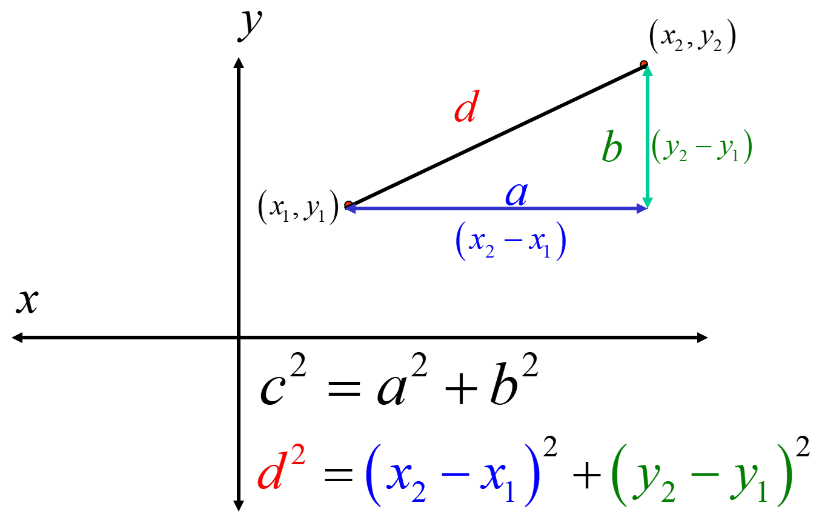
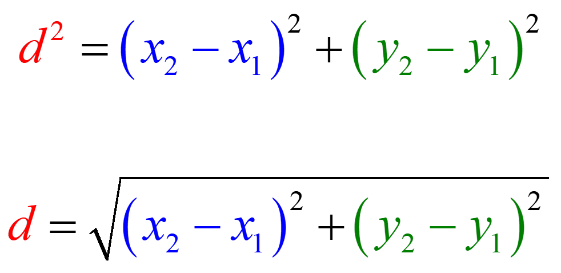
Points dividing a line segment that divide the line segment joining the points (x1, y1) and (x2, y2) by a ratio of m:n can be written as:
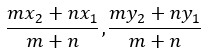
The midpoint of a line segment is used to find the centre of a line segment. The midpoint M of line segment AB is the point that bisects or divides, the segment into two congruent segments. If M is the midpoint of a line segment AB, then AM = MB.
For example, AB = 6, then AM = 3 and MB = 3.
To find the midpoint of two points on a graph we use the following formula:
This is obtained by adding the two x’s and cutting their sum in half. The y’s are also added and then divided by two. The answer can then be written as an ordered pair.
![]()
Area of a triangle
Consider three points in a coordinate plane:(x1,y1), (x2,y2) and (x3,y3)Given the coordinates of the three vertices of any triangle, the area of the triangle is given by:
![]()
It does not matter which points are labelled(x1,y1), (x2,y2) and (x3,y3), this formula will work with any triangle, including those where some or all coordinates are negative. Three points are collinear when the area of their triangle is zero.