Translation – The object is shifted on the plane without changing origin, axis or anything other than location.
| Translation type | Rule |
| Move right by a units | Add a to each x-coordinate: (x,y) |
| Move left by a units | Subtract a from each x-coordinate: (x,y) |
| Move up by b units | Add b to each y-coordinate: (x,y) |
| Move down by b units | Subtract b from each y-coordinate: (x,y) |
To find the change in the coordinates of a point when the origin is shifted to another point but the direction of axes remains unaltered.
If the origin is shifted to point (a, b) then new coordinates points are (x-a, y-b)
For finding the new coordinate of a point after shifting the origin, consider the following cases where axes remain parallel:
Coordinate points: (2, -3) Current origin: (0, 0) and new origin (1, 2)
This is a translation where we move right by 1 unit and up by 2 units. The new coordinates are (1, -5)
Reflection – A ‘mirror’ image is made across the origin and axis.
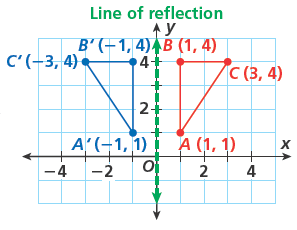
| Type of reflection | Rule |
| Across y-axis | Multiply the x-coordinate by -1: (x, y) |
| Across x-axis | Multiply the y-coordinate by -1: (x, y) |
Rotation – The object is turned like a clock about a fixed point known as the centre of rotation. Center of rotation can be the origin (0,0), the centre of the object, or another point. Rotation is clockwise when its direction is the same as how a clock moves.A rotation in the opposite direction is called counterclockwise while complete rotation is 360˚. A Quarter turn is 90 ˚, the half-turn is 180 ˚, and three-quarter turn is 270 ˚
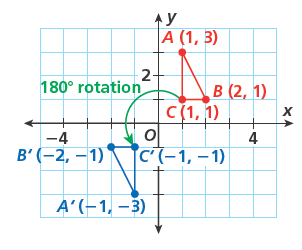
| Type of around the origin | Rule |
| 180 degrees | Multiply both the coordinates by -1: (x, y) |
| 90 degrees clockwise | Multiply each x-coordinate by -1 and then switch the x and y coordinate(x, y) |
| 90 degrees anti-clockwise | Multiply each y-coordinate by -1 and then switch the x and y coordinate(x, y) |
Dilation – The object is made stretched or shrunk but kept centered around the same point. This depends on the factor and the axis. The new coordinate is obtained by multiplying the factor with stretched and dividing when shrunk.
Dilation changes in size only. Reflection changes orientation and position but not size. Translation changes position but not size nor orientation. Rotation changes orientation and position with respect to the center of rotation but not size.