Capacitance Problems

1. Find the equivalent capacitance of system of capacitors shown below.

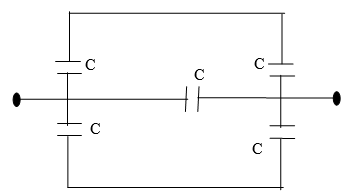
Equivalent capacitance of two capacitors each having capacitance C are connected in series.

So,equivalent capacitance = $C/2$

Therefore, the circuit can be drawn like,

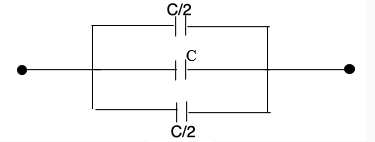
$C/2$, $C$and $C/2$are now in parallel. So the equivalent capacitance,

$C/2$+$C$+ $C/2=2C$

1. Four capacitors are connected as shown below.

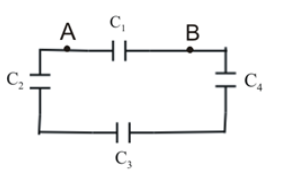
If $C_{1}=2 \mu F$, , $C_{2}=3 \mu F$, $C_{3}=4\mu F$,$ C_{5}=5\mu F$ , calculate the equivalent capacitance between $A$ and $B$.

From the diagram, we can say that capacitors $C_{1}$ $_{ }$and series combination of $C_{2}$, $C_{3}$ and $C_{4}$ are connected in parallel.

If $C”$ is the equivalent capacitance of $C_{2}$, $C_{3}$ and $C_{4}$, then,

$1/C”=1/3+1/4+1/5$

Or, $1/C”=47/60$

Or, $C”=60/47 \mu F$

Now $C” $and $C_{1}$are in parallel.

So, equivalent capacitance, $C=C_{1}+C”=2+60/47=154/47=3.27 \mu F$

2. A point charge $q$ is located at (2, 4, 3) in xyz coordinate. Find the potential difference between A and B if A = (2, 3, 3) and B = (-2, 3, 3).

We have potential at point A,

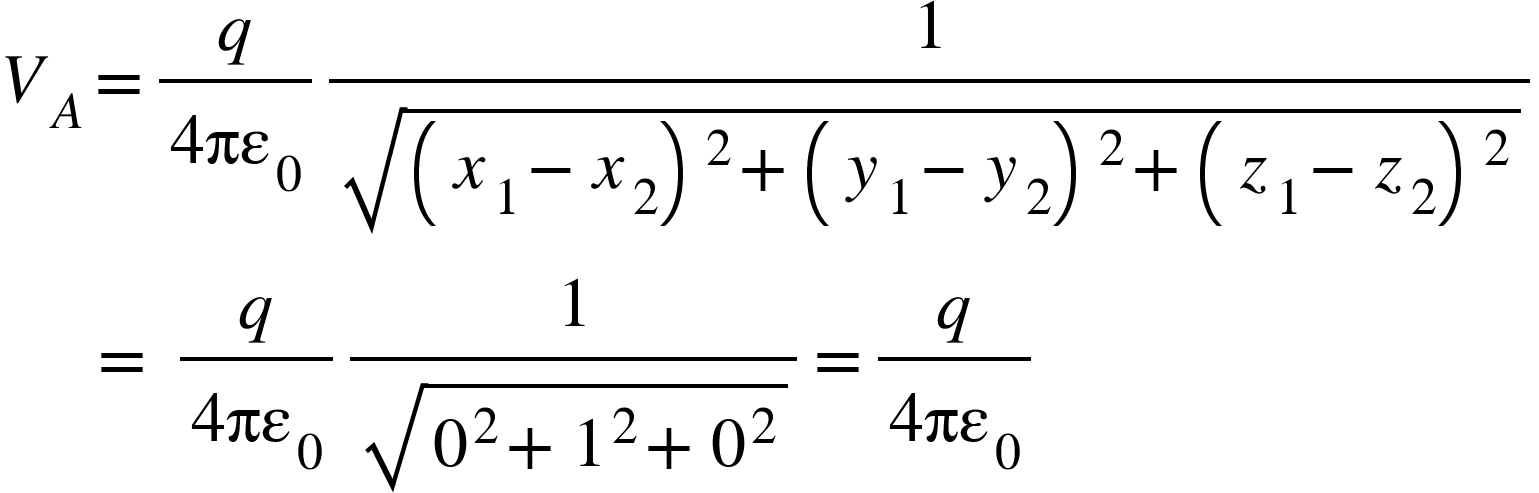
We have potential at point B,

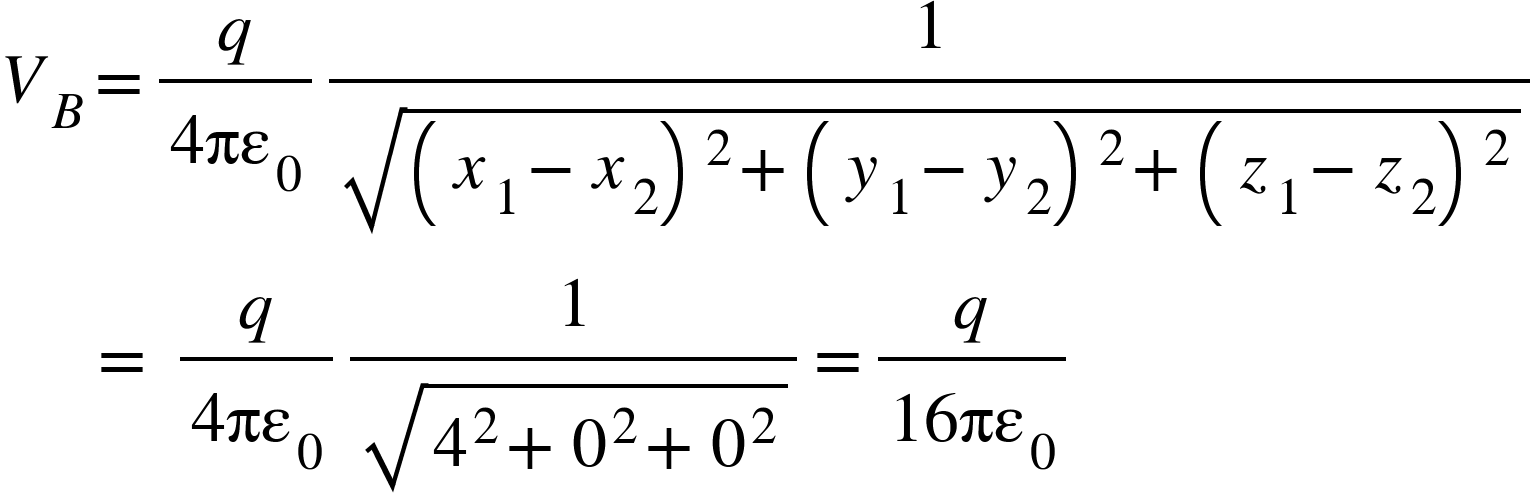
So,

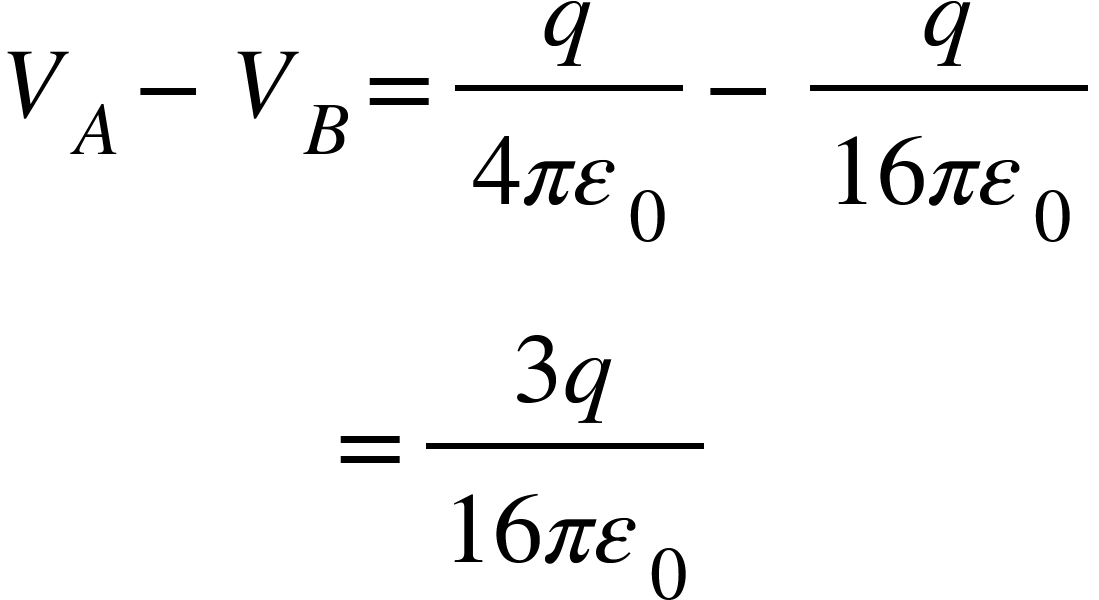
3. A parallel plate capacitor is constructed of metal plates, each of area 0.3 $m^{2}.$ If the capacitance is $8nF$, then calculate the plate separation distance.

We have the equation for parallel plate capacitor,

$C=\epsilon _{0}A/d$

Or, $8\times 10^{-9}=8.85\times 10^{-12}(0.3)/d$

Or, $8d=8.85\times 0.3\times 10^{-3}$

Or, $d=3.32\times 10^{-4}$

Or, $d=0.00032 m=0.32 mm$

4. Refer to the below diagram. Find the resulting capacity of a plate capacitor, if the space between the plates of area S is filled with dielectric with permittivity $\epsilon $.

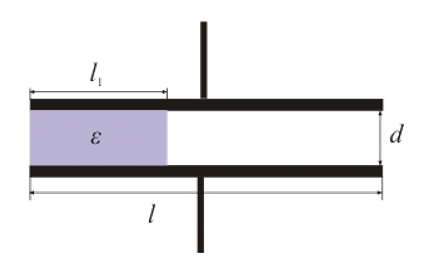
• We will replace the plate capacitor with two that are parallel. One will be filled with dielectric $l_{1}$ wide, the other will be filled with air and $l-l_{1}$wide.
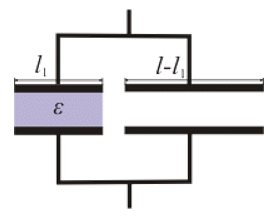
• The total capacity is $C=C_{1}+C_{2}$
• The capacity of a plate capacitor is given by, $C=\epsilon S/d=\epsilon _{0}\epsilon _{r} S/d$
• Therefore, for capacitor $C_{1}$ and $C_{2}$we get,
• $C_{1}=\epsilon _{r} S_{1}/d$ ……………….. (1)
• and $C_{2}=\epsilon _{r} S_{2}/d$ ……………(2)
• Now, we will determine the areas S1 and S2 using the lengths l, l1 and the total area of the capacitors S.The total area of the capacitor is $S= lx$, where x = width of the capacitor
• Then, $S_{1}= l_{1}x$ and $S_{2}=(l- l_{1})x$
• Or, $S_{1}= l_{1}S/l$ and $S_{2}=(l- l_{1})S/l$ (as $S= lx$
• Now, equation (1) becomes, $C_{1}=\epsilon _{r} l_{1}S/dl$
• And equation (2) becomes, $C_{2}=\epsilon _{r} (l- l_{1})S/dl$
• Therefore, the total capacity is $C=C_{1}+C_{2}$
•