Work is done when an object moves a distance by the application of a force.
Consider a block placed on a frictionless horizontal floor. This block is acted upon by a constant force $F$ to move through a distance $d$ in a straight line in the direction of force.
Work done is equal to the product of the magnitude of applied force and the distance through which the body moves.
Mathematically, $W=Fd$ Force active on a block at an angle to the displacement.
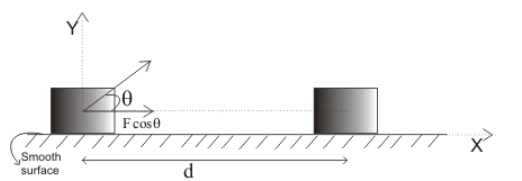
Figure:14.a
If the force $F$ acts at an angle $\theta $ to the displacement $d$, the affective component of force along the direction of displacement is $F cos\theta $F which is responsible for the displacement of the block in the given direction.
So, work done,
$W=\vert F\vert \cos \theta \vert d\vert $
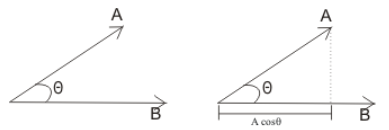
Figure:14.b
From the above diagram, the scalar product of two vectors $
A$ and $B$ where $A$\textbf{ }
makes an angle $\theta $ with $B$ is given by,
$A. B=\vert A\vert \vert B\vert cos \theta $
Work done can be written,
$W=F.d$ .
The SI unit of work done is Joule.
$1J=1Nm$
Work done by variable force:
Work can be done by forces that varies in magnitude and direction during the displacement of the body on which it acts.
Consider the direction of force acting on the body to be along x-axis. Let us assume $\Delta x$ be the small interval of the total displacement.
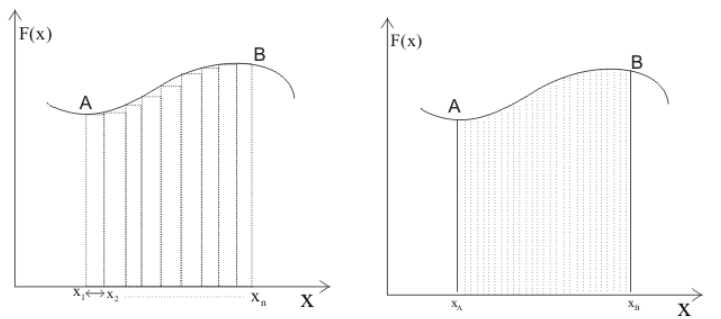
Figure:14.c
Work done in moving the body from x$_{1}$ to x$_{2}$ is given by,$\Delta W=F(x_{1})\Delta x_{1}$, where $\Delta x_{1}=x_{2}-x_{1}$
Total work done in moving the body from point A to point B is given by, $W=F(x_{1})\Delta x_{1}+F(x_{2})\Delta x_{2}+………+F(x_{n})\Delta
x_{n}$
$W=\sum_{i=1}^{n}{}F(x_{i})\Delta x_{i}$
If the displacements are allowed to approach zero, the number of terms in the sum
increases without limit, but the sum approaches a definite value equal to the area under the curve shown below.
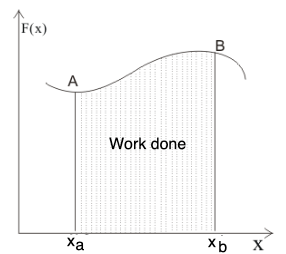
Figure:14.d
Then the work done is,
$W=\lim _{\Delta x\to 0}\sum{}F(x_{i})\Delta x_{i}$
Or, $W=_{x_{a}}^{x_{b}}{}fdx$
Work Energy Theorem:
The relationship between Work and kinetic energy of the object is called the Work Energy Theorem. It states that the net work done on the system is equal to the change in Kinetic energy of the system. $W_{net}=\Delta K$
Where K is the Kinetic Energy of the body
Consider a body of mass moving under the influence of constant force $F$.
From Newton’s second law of motion, we have,$F=m a$
If the velocity of the body increases from $v_{1}$ to $v_{2}$ during the displacement $d$ then we have,
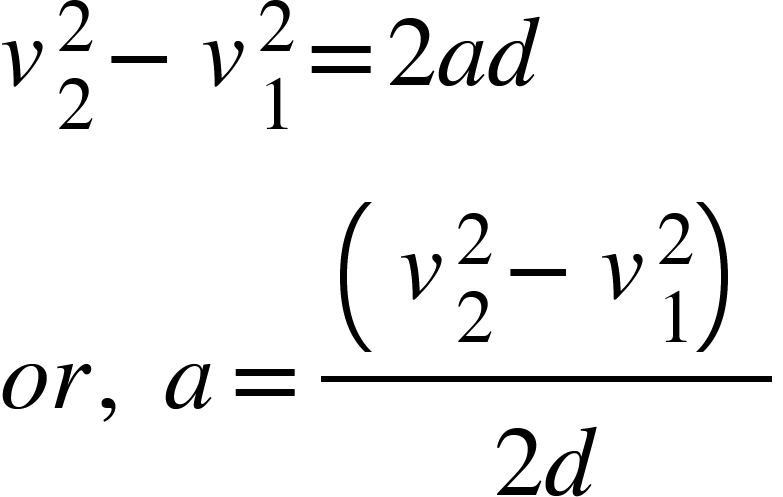
Then,
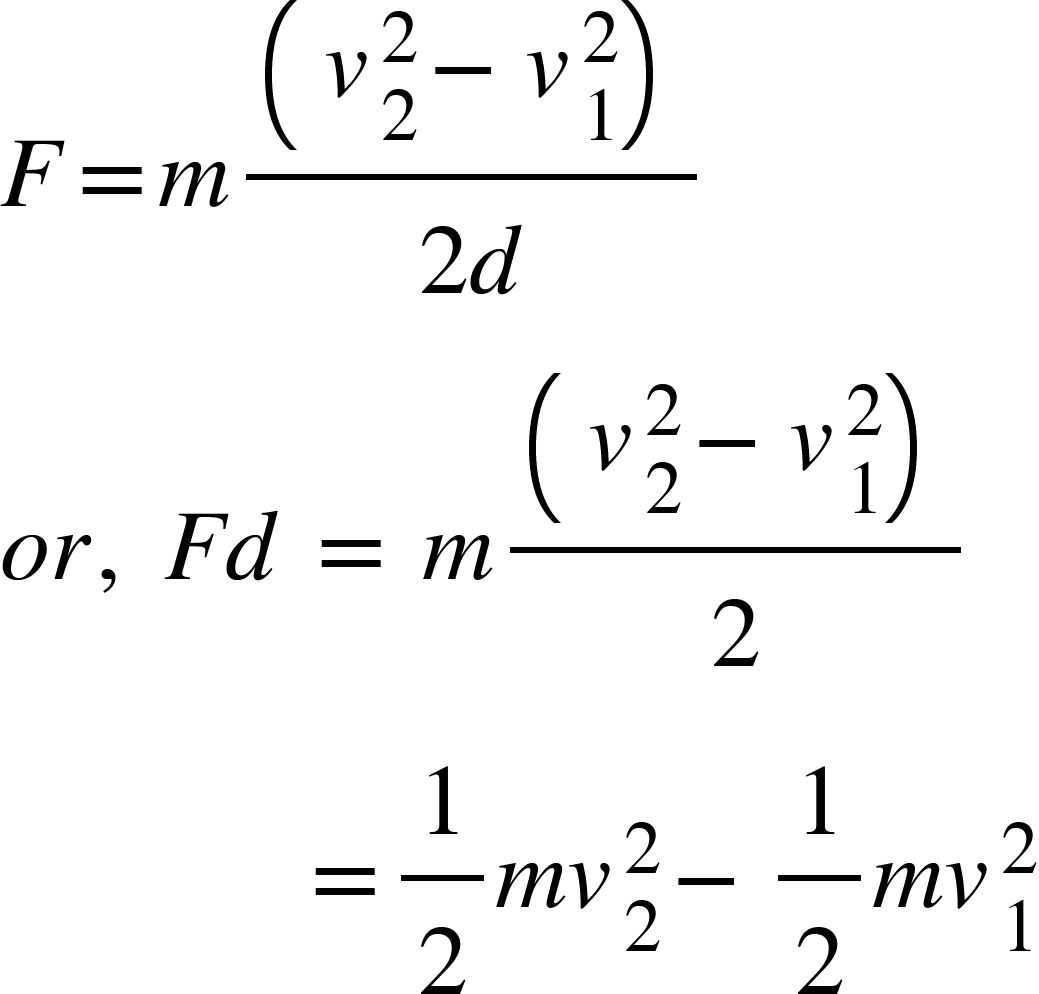
We can write final kinetic energy, $K_{2}=mv_{2}^{2}/2$ and initial kinetic energy, $K_{1}=mv_{1}^{2}/2$
Then,
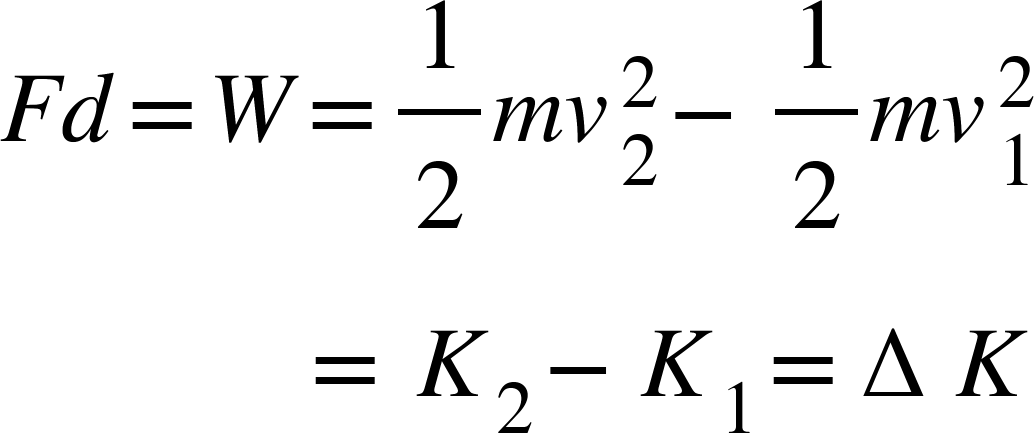
Where $\Delta K$is the change in kinetic energy.
So, work done by a force on a body is equal to the change in kinetic energy of the body.
Points to remember:
- If there are number of forces acting on a body then the resultant force is obtained by the vector sum of all the forces and then find the work done on the body.
- For positive work, kinetic energy increases by the amount of the work and for negative work the final kinetic energy decreases by the amount of work done.