Integrating qλ (T) over all wavelengths from zero to infinity, we obtain by means of expressions for determinate integrals the surface density of the total black-body radiation flux qv (T) as„

Where the Stefan−Boltzmann constant o is equal to the second formula as shown in the above picture.
Similar expressions can also be gained for total radiation intensity„
I (T) = ∫œ q (T, λ) dv = n2 T4
And also for, what is the total volume density of radiation (for vacuum) „
u = ∫œ uv (T,λ)dλ = aT4
0
Where ’a’ is known as radiation density constant.
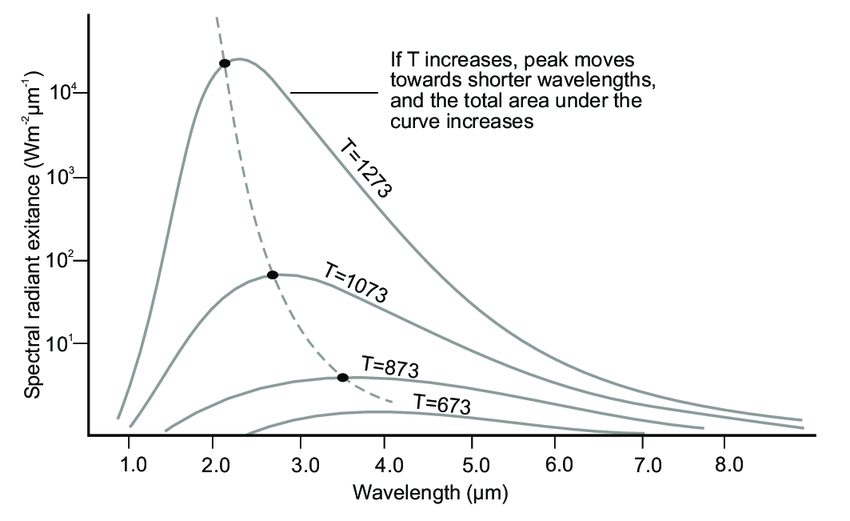
Now consider the instructive example, associated with the relation of the amount of energy, emitted from the unit of the black body’s surface into vacuum within the whole frequency band and in the radio-frequency band separately. Using relations, we obtain the total power, emitted by a black body from 1 square meter at room temperature (300 H), which is equal to 450 U. Now, using the Rayleigh−Jeans law, we obtain the expression for the Stefan−Boltzmann law in the long-wavelength approximation, as follows„
q (T) = 2/3 rk/c2 Tv3
From this expression, we can easily obtain the estimate for the total power emitted by a black body from 1 square meter at Z 300 H throughout the radio-frequency band from 0 frequency up to 1011 Hz. It’s equal to10—4 U. Thus, the rate of energy falling on the entire radio-frequency band is 10—7 times lower than black-body radiation with its full power. As a result, an even smaller part (10—9) of the total power will be expected to fall on the whole, for example, the centimeter band. And, despite of such small values of radiation power in the radio-frequency band, the modern microwave remote radio systems are able to successfully record such low levels of a thermal signal.
Derivation of Stefan Boltzmann Law
The total power radiated per unit area over all wavelengths of a black body is obtained by integrating Plank’s radiation formula. Thus, the radiated power per unit space as a function of wavelength is:
dPdλ1A=2πhc2λ5 (ehcλkT−1)
Where,
P is Power radiated.
A is the surface area of a blackbody.
Λ is the wavelength of emitted radiation.
h is Planck’s constant
c is the velocity of light
k is Boltzmann’s constant
T is temperature.
On simplifying Stefan Boltzmann equation, we get:
d (PA) dλ=2πhc2λ5 (ehcλkT−1)
On integration each the perimeters with reference to λ and applying the limits we get;
∫∞0d (PA) dλ=∫∞0⎡⎣⎢2πhc2λ5 (ehcλkT−1) ⎤⎦⎥dλ
The integrated power after separating the constants is:
PA=2πhc2∫∞0⎡⎣⎢dλλ5 (ehcλkT−1) ⎤⎦⎥— (1)
This can be solves analytically by substituting:
x = hcλkT
Therefore, dx=−hcλ2kTdλ
⇒ h=xλkTc
⇒ c=xλkTh
⇒ dλ=−λ2kThcdx
As a results of substituting them in equation (1)
⇒PA=2π (xλkTc) (xλkTh) 2∫∞0 [(−λ2kThc) dxex−1]
= 2π (x3λ5k4T4h3c2λ5) ∫∞0 [dxex−1]
=2π (kT) 4h3c2∫∞0 [x3ex−1] dx
The above equation is similar to the quality style of integral:
∫∞0 [x3ex−1] dx=π415
Thus, substituting the above result we get,
PA=2π (kT) 4h3c2π415⇒PA= (2k4π515h3c2) T4
On further simplifying we get,
⇒ P/A = σ T4
Thus, we reach a mathematical kind of Stefan Boltzmann law:
⇒ε = σT4
Where,
ε = P/A
σ= (2k4π515h3c2) = (5.670×108wattsm2K4)
This quantum-mechanical result might expeditiously express the behavior of gases at low temperatures that mechanics couldn’t predict.