The mirror formula can be defined as a formula that describes the relationship between the distance of object u, a distance of image v, and the focal length of the mirror. The mirror formula is applicable for both spherical mirrors and plane mirrors. In mathematic form, it can be written as follows.
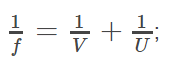
When an object is placed in front of the mirror, then an image is formed. If the light rays from the object are falling on the mirror, and then they are reflected and converged to make an image, the image formed is a real image. But if there is no converging of the reflected light rays, then the image is virtual. Mirror formula is extremely important in these aspects. To get exact information, about magnification and size of the image, and distance of the image from the spherical mirrors, the mirror formula can be used for exact understanding.
Sometimes, the magnification formula is also used instead of a mirror formula. The specifications for this formula are similar to some extent to the mirror formula. As the heights above the principal axis are positive and below the axis are negative. The positive magnification is also above the axis, and negative magnification is below the axis.
Assumptions
- For the derivation of mirror formula, some assumptions are taken which are stated below.
- The measurement of distances is from poles of mirrors.
- The size of the aperture of the mirror is small.
- According to the convention, a negative sign is an indication that the measured distance in the opposite direction, to the incident ray. Whereas, the positive sign indicates that the measurement of distance is in the direction of the incident ray.
- The distance above the axis is always positive, while distance, below the axis, is negative.
Derivation of Mirrors Formula
The mirror formula can be derived as described in the below section. The below diagram is greatly helpful for understanding the derivation of the mirror formula.

The given diagram shows that an object AB is placed at some distance U, from point p, that is the pole of the mirror. By looking at the diagram it can be said that there is the formation of image A1B1, at a point V from the mirror. In this diagram, it is clear that according to the law of vertically opposite angles the opposite angles are equal. So, the following condition can be written.







This formula can be used, for all kinds of spherical mirrors, and all the positions of objects. But for deriving its values, one needs to be careful.